S13 Confidence intervals
We use the statistics we obtain from samples to make inferences or estimates about the population from which the sample was drawn.
For example:
A batch may be selected in a factory production process to assess how the process is operating.
Surveys of consumers are used to determine the preferred brands in the population.
Polls are conducted on samples of the voting population before elections to predict the result of the election.
Confidence Intervals
Together with our estimate of the population parameter it is often helpful to provide a confidence interval. After constructing a confidence interval we are able to make statements such as: “we are \(95\)% confident that the true mean weight of boxes of cocobix cereal labelled \(450\)g is in the interval \([449.5,453.8]\)”.
For large samples (\(n\geq30\)) we can use the mean of a sample, \(\overline{x}\), to find an interval estimate for the mean of the population, \(\mu\), using the formula:
\[\begin{align*} \mu & =\overline{x}\pm z\times\frac{\sigma}{\sqrt{n}}\qquad\textrm{or}\qquad\mu=\overline{x}\pm z\times\frac{s}{\sqrt{n}}\qquad\textrm{when}\;\sigma\;\textrm{is not known} \end{align*}\]
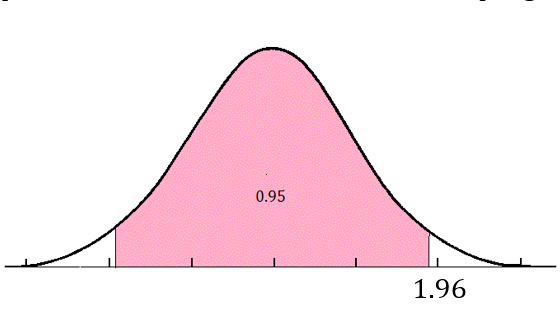
The value of \(z\) is determined by the level of confidence and can be found using normal tables, a graphics calculator or an online statistics program.

For a \(95\)% confidence interval, \(z=1.96\)
For a \(99\)% confidence interval, \(z=2.575\)
For a \(90\)% confidence interval, \(z=1.645\)
Example
\(36\) of a certain type of fish were caught in Port Phillip Bay. This sample had a mean length of \(30\) cm. and a standard deviation of \(3\) cm.
What is the \(95\)% confidence interval for the true mean length of this type of fish?
What is the \(98\)% confidence interval for the true mean length of this type of fish?
Solution:
\(95\)% confidence interval for \(\mu\) \[\begin{align*} & =\overline{x}\pm z\times\frac{s}{\sqrt{n}}\\ & =30\pm1.96\times\frac{3}{\sqrt{36}}\\ & =30\pm0.98\\ & =\left[29.02,30.98\right] \end{align*}\] We can state with \(95\)% confidence that the mean of the entire population of fish will be between \(29.02\)cm and \(30.98\)cm
\(98\)% confidence interval for \(\mu\) \[\begin{align*} & =\overline{x}\pm z\times\frac{s}{\sqrt{n}}\\ & =30\pm2.326\times\frac{3}{\sqrt{36}}\\ & =30\pm1.163\\ & =\left[28.84,31.16\right] \end{align*}\] We can state with \(98\)% confidence that the mean of the entire population of fish will be between \(28.84\) cm and \(31.16\) cm.
Exercises
1. In an effort to improve appointment scheduling, a doctor agreed to estimate the average time spent with each patient. A random sample of \(49\) patients yielded a mean of \(30\) minutes and a standard deviation of \(7\) minutes.
Construct a \(95\)% confidence interval for the true mean.
Construct an \(80\)% confidence interval for the true mean.
(a) \([28.04,31.96]\quad\)(b) \([28.72,31.28]\)
2. To estimate the average weight of males in the town of Cityville a random sample of \(100\) men was drawn from the population of \(10,000\) men and weights recorded. The mean weight was found to be \(83\) kg and the standard deviation \(12\) kg.
What is the \(99\)% confidence interval for the mean weight of the male population?
In two of the suburbs of Cityville, Subtown and Tubtown, the mean weights for males were found to be \(80\)kg and \(88\)kg repectively. Comment on these results.
(a) \(\left[79.91,86.09\right]\quad\)(b) The mean weight for Subtown men is within the expected range but men who live in Tubtown appear to be extremely heavy compared with the general population. This may reflect lifestyle differences or a failure to select a random and representative sample.
3. A market research company conducted a randomised survey of \(50\) regular smokers to find the amount spent on cigarettes per week. They found that the smokers spent on average $ \(22\) each week and the standard deviation was $ \(4.50\). Using a \(95\)% level of confidence calculate the confidence interval for the true mean amount spent on cigarettes by regular smokers.
\([20.75,23.25]\)
4. After randomly sampling \(400\) individuals and obtaining a sample mean of \(56.5\) a research company was able to claim they were \(90\)% certain that the true mean of the population was between \(56.089\) and \(56.911\). What was the standard deviation of the sample?
5
Download this page: S13_Confidence_Intervals (PDF 1.907KB)
What's next... S14 Hypothesis testing
