M1 Matrices: Introduction

July 14, 2021 - 11:00am — AJ (e67821)

Open image

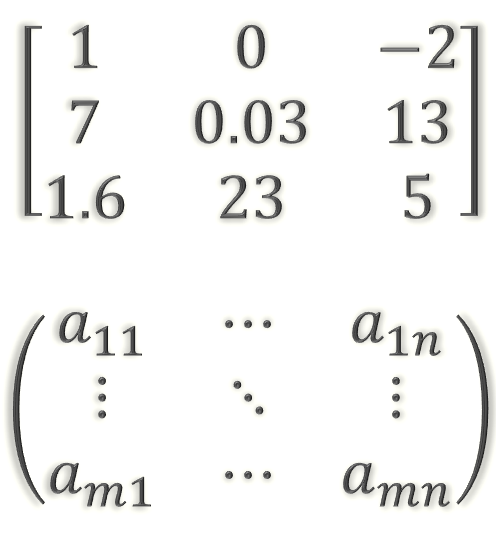
A matrix is a rectangular array of elements.
Matrices are usually denoted by upper case letters.
The elements are usually written within brackets.
The order or shape of the matrix is determined by the number of rows and columns of the matrix.
The number of rows is always given first then the number of columns. Example. \[\begin{align*} A & =\left[\begin{array}{ccc} 1 & 2 & -9\\ 2 & 5 & -3 \end{array}\right] \end{align*}\]

$A$ has 2 rows and 3 columns and is called a $2\times3$ matrix.11 This is verbally stated as a 2 by 3 matrix.

A matrix with $m$ rows and $n$ columns is called a matrix of order $m\times n$.22 This is verbally termed an “m by n matrix”.

Square Matrix

A matrix with the same number of rows and columns is called a square matrix.

Example: \[\begin{align*} B & =\left[\begin{array}{cc} 2 & 3\\ 2 & 5 \end{array}\right] \end{align*}\]

$B$ is a square $2\times2$ matrix

Unit Matrix

A unit (or identity) matrix is a square matrix with diagonal elements equal to one, and all other elements equal to zero. The unit matrix is usually denoted by $I$.

$I_{3}$ is a $3\times3$ unit matrix

Example: \[\begin{align*} I_{3} & =\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] \end{align*}\]

Row Matrix

A matrix with one row is called a row matrix.

Example: \[\begin{align*} D & =\left[\begin{array}{cccc} 2 & 1 & 0 & 4\end{array}\right] \end{align*}\] is a $1\times4$ row matrix

Column Matrix

A matrix with one column is called a column matrix.

Example: \[\begin{align*} E & =\left[\begin{array}{c} 2\\ -4\\ 1 \end{array}\right] \end{align*}\]

is a $3\times1$ column matrix

Zero Matrix

A zero matrix has all elements equal to zero. A zero matrix can be written as $0$.

Example: \[\begin{align*} 0 & =\left[\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right] \end{align*}\]

is a $2\times2$ zero matrix

Equal Matrices

For two matrices to be equal, they must be the same shape and the corresponding elements must be equal.

If $A$ equals $B$ then \[\begin{align*} A & =\left[\begin{array}{ccc} 2 & 5 & b\\ 5 & 3 & 1\\ 2 & 0 & -2 \end{array}\right] & B & =\left[\begin{array}{ccc} 2 & 5 & 7\\ 5 & a & 1\\ 2 & 0 & -2 \end{array}\right] \end{align*}\]

If $A$ and $B$ are equal then $a$ = 3 and $b$ = 7.

Exercise:

Write down the order of the following matrices.

$\left[\begin{array}{ccc} 7 & -5 & 0\\ 6 & 2 & -1 \end{array}\right]$
$\left[\begin{array}{cc} 0 & 2\\ 1 & 1 \end{array}\right]$
$\left[\begin{array}{c} 2\\ -4\\ 1\\ 1 \end{array}\right]$
$\left[\begin{array}{cc} 1 & 1\\ 3 & 0\\ -2 & 3 \end{array}\right]$

Which of the following matrices are equal?

\[\begin{align*} A & =\left[\begin{array}{cc} 3 & 0\\ 1 & -2 \end{array}\right] & B & =\left[\begin{array}{cc} 3 & 1\end{array}\right] & C & =\left[\begin{array}{cc} 3 & 0\end{array}\right] & D & =\left[\begin{array}{cc} 3 & 0\\ 1 & -2 \end{array}\right] \end{align*}\]

\[\begin{align*} E & =\left[\begin{array}{ccc} 3 & 5 & 1\\ 2 & 0 & 1 \end{array}\right] & F & =\left[\begin{array}{cc} 0 & 3\end{array}\right] & G & =\left[\begin{array}{ccc} 3 & 5 & 1\\ 2 & 0 & 1\\ 1 & 3 & 0 \end{array}\right] \end{align*}\]