ILS1.2 Fractional indices
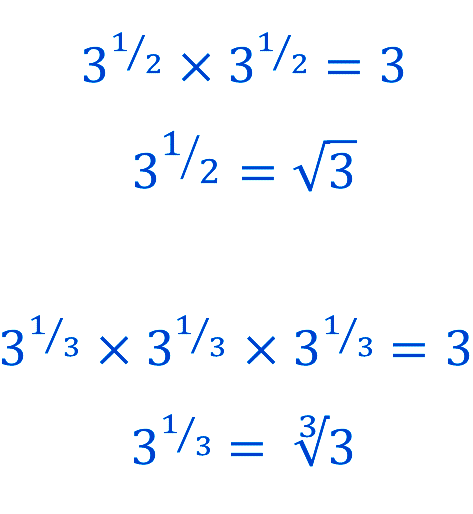
Can an index also be a fractional number?
An index can be an integer – a counting number - either positive or negative.
An index can also be a fraction such as ½, ¾, or 2.5.
Read this section to see what this means, and how the laws of indices apply to fractional indices.
In another module, the index laws were introduced and example were given of their application. The actual indices were whole numbers. But the index laws also work with fractional indices. In this module we introduce fractional indices and give some meaning to numbers and expressions like \(3^{1/3}\)or \(x^{1/2}\).
Index Laws
Remember the basic index laws:
\(\quad\quad\) \(a^{m}\times a^{n}=a^{m+n}\)
\(\quad\quad\) \(a^{m}\div a^{n}=a^{m-n}\)
\(\quad\quad\) \(\left(a^{m}\right)^{n}=a^{mn}\)
\(\quad\quad\) \(a^{0}=1\)
\(\quad\quad\) \(a^{-n}=\frac{1}{a^{n}}\)
These hold when \(m\) and \(n\) are whole numbers or fractions. In what follows, we will refer to these as the first index law, the second index law etc.
Fractional Indices
What meaning can we give to \(3^{1/2}.\) Using the first index law, we find: \[\begin{align*} 3^{1/2}\times3^{1/2} & =3^{1/2+1/2}\\ & =3^{1}\\ & =3. \end{align*}\] So \(3^{1/2}\) is the number that when multiplied by itself, gives three. But the square root of \(3\) is the number that when multiplied by itself gives \(3.\) That is: \[\begin{align*} \sqrt{3}\times\sqrt{3} & =3. \end{align*}\] Since \(3^{1/2}\) behaves like \(\sqrt{3}\) we say \[ 3^{1/2}=\sqrt{3}. \]
Consider now \(2^{1/3}\). Using the first index law, we can write: \[\begin{align*} 2^{1/3}\times2^{1/3}\times2^{1/3} & =2^{1/3+1/3+1/3}\\ & =2^{1}\\ & =2. \end{align*}\] So \(2^{1/3}\) behave like the cube root of \(2.\) That is, \[\begin{align*} 2^{1/3} & =\sqrt[3]{2} \end{align*}\]
In general we say that \(a^{1/n}\) is the \(n^{th}\) root of \(a.\) That is \[ a^{1/n}=\sqrt[n]{a} \] for any positive integer \(n\) (whole numbers like \(1,2,\ldots\) ).
Examples
\(\qquad4^{1/2}=\sqrt{4}=2.\)
\(\qquad27^{1/3}=\sqrt[3]{27}=3.\)
\(\qquad3^{1/4}=\sqrt[4]{3}.\)
\(\qquad b^{1/5}=\sqrt[5]{b}.\)
\(\qquad x^{1/2}=\sqrt{x}.\)
\(\qquad32^{-1/5}=\frac{1}{32^{1/5}}=\frac{1}{\sqrt[5]{32}}=\frac{1}{2}.\)
In most cases the root of a number will not be able to be written as a whole number or fraction and will be an irrational number. For example \(\sqrt{2}=1.41421356\ldots\).
For some practice, please do Exercise 1
Exercise 1
Evaluate the following expressions. If the answer is not exact, use a calculator to give a decimal approximation to two decimal places.
a)\(\;64^{1/2}\) \(\quad\quad\) b) \(\;125^{1/3}\) \(\quad\quad\)c) \(\;36^{1/4}\) \(\quad\quad\)d) \(\;81^{-1/2}\) \(\quad\quad\)e) \(\;128^{-1/7}\) \(\quad\quad\)f) \(\;250^{1/5}\)
\[\begin{array}{lllllllllll} a)\;8 & & b)\;5 & & c)\;2.45 & & d)\;1/9 & & e)\;1/2 & & f)\;3.02\end{array}\]
More Complicated Fractional Indices
In this section, we introduce terms like \(a^{2/3}\).
Using the third index law1 The third law is: \(\left(a^{m}\right)^{n}=a^{mn}\) we have: \[\begin{align*} a^{2/3} & =\left(a^{2}\right)^{1/3}\\ & =\sqrt[3]{a^{2}}\quad\textrm{using the definition of indices as roots.} \end{align*}\]
Again using the third index law:2 We use the commutative law: \[\begin{align*} mn & =m\times n\\ & =n\times m\\ & =nm. \end{align*}\] In our case, we are using the fact that \(2\times\left(1/3\right)=\left(1/3\right)\times2.\) \[\begin{align*} a^{2/3} & =a^{2\times\left(1/3\right)}\\ & =a^{\left(1/3\right)\times2}\\ & =\left(\sqrt[3]{a}\right)^{2}. \end{align*}\]
In general, \[\begin{align*} a^{p/q} & =\sqrt[q]{a^{p}} \end{align*}\] or \[\begin{align*} a^{p/q} & =\left(\sqrt[q]{a}\right)^{p} \end{align*}\] where \(p\) and \(q\) are integers with \(q\neq0.\)
Examples
\(\quad\quad\) \(5^{\frac{3}{4}}\)=\(\sqrt[4]{5^{3}}\)or \(\left(\sqrt[4]{5}\right)^{3}\).
\(\quad\quad\) \(7^{5/2}\) = \(\sqrt{7^{5}}\) = \(\left(\sqrt{7}\right)^{5}\).
\(\quad\quad\) \(a^{7/5}\) = \(\sqrt[5]{a^{7}}\)= \(\left(\sqrt[5]{a}\right)^{7}\).
\(\quad\quad\) \(y^{-\frac{3}{4}}\) = \(\frac{1}{y^{\frac{3}{4}}}\) = \(\frac{1}{\sqrt[4]{y^{3}}}\) or \(\frac{1}{\left(\sqrt[4]{y}\right)^{3}}\) .
Using the fifth index law: The fifth law is \(a^{-n}=\frac{1}{a^{n}}\).
- \(\quad\quad\) \(\sqrt[4]{x^{3}}=x^{3/4}.\)
Simplification of Expressions
The index laws may be used to simplify algebraic expressions as shown in the following examples. Note that you don’t have to put in the lines of text explaining each step.
- Simplify \(\left(x^{3}y^{9}\right)^{2/3}.\)
Solution:
The third index law is: \[ \left(a^{m}\right)^{n}=a^{mn} \]
\[\begin{align*} \left(x^{3}y^{9}\right)^{2/3} & =x^{3\times\left(2/3\right)}y^{9\times\left(2/3\right)}\quad\textrm{using the third law,}\\ & =x^{2}y^{6}. \end{align*}\]
- Simplify \(3^{1/3}\div3^{4/3}.\)
Solution:
The second index law is: \[ a^{m}\div a^{n}=a^{m-n}. \]
\[\begin{align*} 3^{1/3}\div3^{4/3} & =3^{\left(1/3\right)-\left(4/3\right)}\quad\textrm{using the second index law,}\\ & =3^{-\left(3/3\right)}\\ & =3^{-1}\\ & =\frac{1}{3}. \end{align*}\]
- Simplify \(32^{3/5}\).
Solution:
For this example, you need to know the fifth root of \(32\) is \(2\) . In symbols \(\sqrt[5]{32}=2.\) That is \(2\times2\times2\times2\times2=32.\)
\[\begin{align*} 32^{3/5} & =\left(\sqrt[5]{32}\right)^{3}\\ & =2^{3}\\ & =8. \end{align*}\]
- Simplify \(25^{-1/2}.\)
Solution:
For this example you need to know the square root of 25 is 5. In symbols \(\sqrt{25}=5.\) That is \(5\times5=25\). You also need to use index law 5: \[ a^{-n}=\frac{1}{a^{n}}. \]
\[\begin{align*} 25^{-1/2} & =\frac{1}{\sqrt{25}}\quad\textrm{using index law 5,}\\ & =\frac{1}{5} \end{align*}\]
- Simplify \(\left(a^{2}b^{5}\right)^{1/3}\times a^{1/3}b^{-2/3}.\)
Solution: \[\begin{align*} \left(a^{2}b^{5}\right)^{1/3}\times a^{1/3}b^{-2/3} & =a^{2/3}b^{5/3}\times a^{1/3}b^{-2/3}\quad\textrm{using the third index law,}\\ & =a^{\left(2/3\right)+\left(1/3\right)}b^{\left(5/3\right)-\left(2/3\right)}\\ & =ab. \end{align*}\]
Please do Exercise 2 for some practice.
Exercise 2
Simplify the following expressions. Give your answers in index notation with positive indices.
a)\(\left(\frac{8}{27}\right)^{2/3}\quad\) b)\(\sqrt{5}\times\sqrt[3]{5}\times\sqrt[6]{5}\quad\) c) \(\sqrt{a}\times\sqrt[4]{a}\times\sqrt[3]{a^{2}}\quad\) d) \(\left(125a^{6}b\right)^{1/3}\times b^{2/3}\quad\) e) \(\frac{\left(2xy^{3}\right)^{1/2}}{2}\times\left(\frac{x^{3/2}}{y^{2}}\right)^{4}\quad\) f) \(2^{5/2}-2^{3/2}\)
\[\begin{array}{lllllllllll} a)\;\frac{2^{2}}{3^{2}} & & b)\;5 & & c)\;a^{17/12} & & d)\;\text{5$a^{2}$ b} & & e)\;\frac{x^{13/2}}{2^{1/2}y^{13/2}} & & f)\;2^{3/2}\end{array}\]
What's next... ILS2.1 Logarithms
