V8 Equation of a plane
Learn how to find the equation of a plane (a 2-dimensional space):
a) through three points or
b) given a normal (line at right angles) and a point on the plane or
c) given a parallel plane and a point on the plane.
(See also Linear graphs)
A plane is a subset of three dimensional space. In non mathematical terms you can think of it as a flat surface that extends infinitely in two directions. It may be defined as
the surface that goes through three points or
the surface containing a point and having a fixed normal vector.
Cartesian Equation of a Plane
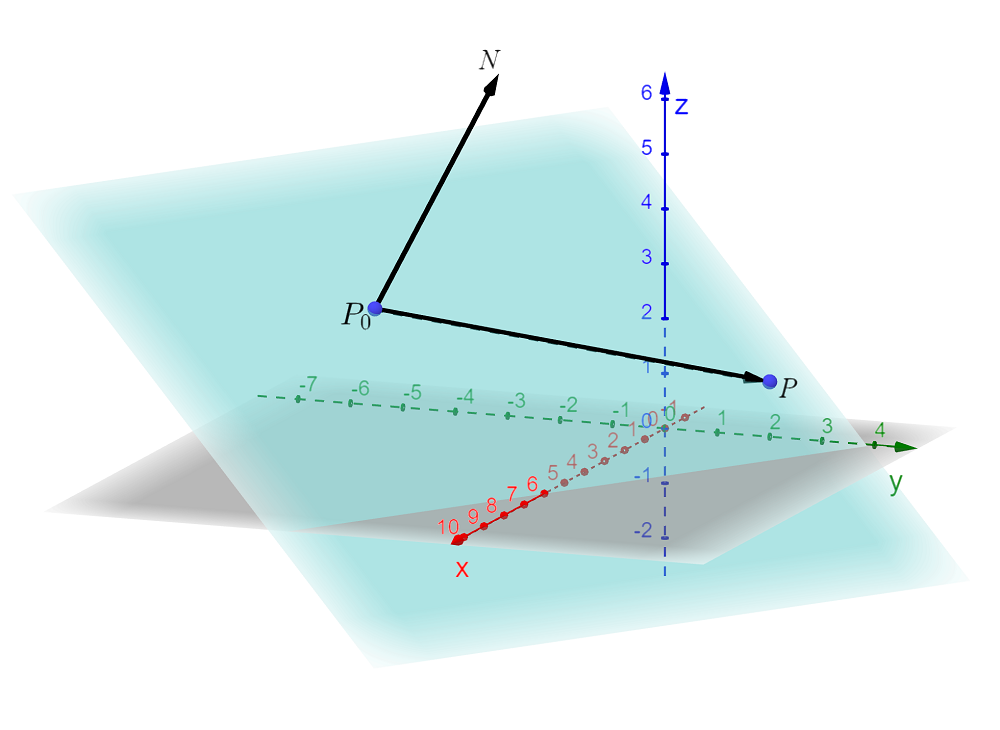
The above diagram represents a part of a plane. On the plane are two points, \(P(x,y,z)\) and \(P_{0}(x_{0},y_{0},z_{0})\) .
The vector \(\overrightarrow{P_{0}P}=(x-x_{0})\hat{i}+(y-y_{0})\hat{j}+(z-z_{0})\hat{k}\).
Also illustrated is a normal vector to the plane (that is a vector at right angles to the plane) represented by \(\overrightarrow{N}=a\hat{i}+b\hat{j}+c\hat{k}\), where \(a,b\) and \(c\) are constants.
Since \(\overrightarrow{N}\) is perpendicular to \(\overrightarrow{P_{0}P}\) their dot product must equal zero,1 The definition of the dot product of two vectors \(\vec{a}\) and \(\vec{b}\) is \[\begin{align*} \vec{a}\cdot\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\cos\theta \end{align*}\] where \(\theta\) is the angle between \(\vec{a}\) and \(\vec{b}\). If \(\vec{a}\) and \(\vec{b}\) are perpendicular, \(\theta=90^{\circ}\). Hence \(\cos\left(\theta\right)=\cos\left(90^{\circ}\right)=0\) and so \[\begin{align*} \vec{a}\cdot\vec{b} & =0. \end{align*}\] that is to say \(\overrightarrow{N}.\overrightarrow{P_{0}P}=0\) therefore:
\[\begin{align*} \left(a\hat{i}+b\hat{j}+c\hat{k}\right).\left((x-x_{0})\hat{i}+(y-y_{0})\hat{j}+(z-z_{0})\hat{k}\right) & =0 \end{align*}\]
So
\[\begin{align*} a(x-x_{0})+b(y-y_{0})+c(z-z_{0}) & =0. \end{align*}\]
This equation defines the plane in Cartesian coordinates.
This equation may be rearranged: \[\begin{align*} a(x-x_{0})+b(y-y_{0})+c(z-z_{0}) & =0\\ ax+by+cz & =ax_{0}+by_{0}+cz_{0}\\ & =d \end{align*}\] where \(d\) is a constant. In fact, the general equation of a plane with the normal vector \(\overrightarrow{N}=a\hat{i}+b\hat{j}+c\hat{k}\) is \[\begin{align*} ax+by+cz & =d. \end{align*}\]
For example,
1. \(\;2x-3y+z=6\) is a plane.
2.\(\;x+y=4\) is a plane.
3.\(\;z=x-2y+3\) is a plane. To see this rearrange it to get the Cartesian form of the plane, \(x-2y-z=-3\).
Example 1
If a plane has the normal vector \(\overrightarrow{N}=\hat{i}+2\hat{j}-5\hat{k}\) and contains the point \((3,4,1)\) then we can say that the equation of the plane is: \[\begin{align*} 1(x-3)+2(y-4)-5(z-1) & =0\\ x-3+2y-8-5z+5 & =0\\ x+2y-5z & =3+8-5\\ x+2y-5z & =6 \end{align*}\]
Compare this equation with the normal vector, \(\overrightarrow{N}\). You will notice that the coefficients of \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) for the normal vector are the same as the coefficients of \(x,y\) and \(z\) in the equation of the plane.
Example 2
Find the equation of the plane normal to the vector \(6\hat{i}-5\hat{j}+\hat{k}\) that passes through the point \((1,2,3)\).
The equation of the plane will be 2 Obviously there are an infinite number of parallel planes that are perpendicular to the given vector. For instance \(6x-5y+z=-1\) , \(6x-5y+z=0\) , \(6x-5y+z=6\) , \(6x-5y+z=11\) etc. are all perpendicular to the vector \(6\hat{i}-5\hat{j}+\hat{k}\) but only one of these, \(6x-5y+z=-1\) , will pass through the given point. \[\begin{align*} 6(x-1)-5(y-2)+1(z-3) & =0\\ 6x-6-5y+10+z-3 & =0\\ 6x-5y+z & =6-10+3\\ 6x-5y+z & =-1 \end{align*}\]
Not only can we find the equation of a plane, given a point and a normal vector, but we can also find the equation of the normal vector given the equation of a plane.
For example the plane \(3x+4y-z=9\) has a normal vector \(\overrightarrow{N}=3\hat{i}+4\hat{j}-\hat{k}\).
Example 3
Find the equation of the plane that passes through the point \((2,1,-5)\) and is parallel to the plane \(z=2x+3y-4\) .
Since the plane is parallel to \(z=2x+3y-4\) , it will have the same normal vector.
The equation \(z=2x+3y-4\) can be written as \(2x+3y-z=4\) , therefore its normal vector will be \(2\hat{i}+3\hat{j}-\hat{k}\) .
So the equation of the plane we wish to find will pass through the point \((2,1,-5)\) and have a normal vector \(2\hat{i}+3\hat{j}-\hat{k}\) .
\[\begin{align*} 2(x-2)+3(y-1)-1(z+5) & =0\\ 2x-4+3y-3-z-5 & =0\\ 2x+3y-z & =4+3+5\\ 2x+3y-z & =12 \end{align*}\]
Example 4
Find the equation of the plane that contains the three points \(A(1,1,1)\) , \(B(2,4,3)\) and \(C(3,2,1)\) .
First find the cross product of the vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\) as this will give a vector normal to the plane.
Then use this normal vector and any one of the three given points to find the equation of the plane.
\(\overrightarrow{AB}\times\overrightarrow{AC}=(\) \(1\hat{i}+3\hat{j}+2\hat{k})\times(2\hat{i}+\hat{j})\)
\(=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ 1 & 3 & 2\\ 2 & 1 & 0 \end{array}\right|=-2\hat{i}+4\hat{j}-5\hat{k}\)
So the plane has the normal vector \(\overrightarrow{N}=-2\hat{i}+4\hat{j}-5\hat{k}\) and contains the point \((1,1,1)\)3 Either of the other two points could also have been used
Therefore the equation of the plane is
\[\begin{align*} -2(x-1)+4(y-1)-5(z-1) & =0\\ -2x+2+4y-4-5z+5 & =0\\ -2x+4y-5z & =-2+4-5\\ -2x+4y-5z & =-3\\ \textrm{or $2x-4y+5z$ } & =3. \end{align*}\]
Exercises
- What are the vectors normal to the following planes,
\(2x+3y+7z=13\)
\(z=x+3y-9.\)
Answer: a) \(2\hat{i}+3\hat{j}+7\hat{k}\qquad\)b) \(\hat{i}+3\hat{j}-\hat{k}\).
Find the equation of the plane that contains the point \((2,3,1)\) and has the normal vector \(4\hat{i}+3\hat{j}-2\hat{k}.\)
Answer: \(4x+3y-2z=15\).Find the equation of the plane that contains the point \((5,-3,2)\) and has the normal vector \(\hat{i}-9\hat{j}-4\hat{k}.\)
Answer: \(x-9y-4z=24\).Find the equation of the plane that contains the point \((1,-1,0)\) and is parallel to the plane \(x-3y+2z=0.\)
Answer: \(x-3y+2z=4\).Find the equation of the plane that contains the points \((1,2,3)\) , \((2,1,1)\) and \((-3,0,4).\)
Answer: \(5x-7y+6z=9\) .
Download this page: V8 Equations of a plane (PDF 401KB)
What's next... V9 Intersecting planes
