V3 Scalar product
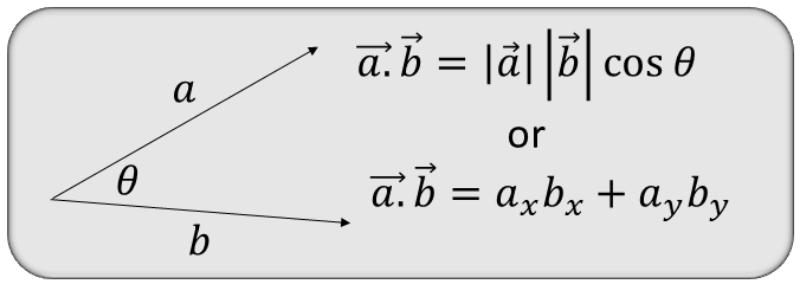
What is a scalar product? What is a dot product? This is the result of multiplying the magnitudes of the components of two or more vectors. The result is not a vector, but a scalar (which is without direction).
There are two ways to multiply two vectors:
The scalar or dot product which gives a number;
The vector or cross product which gives a vector.
In this module we consider the scalar or dot product.
Definition
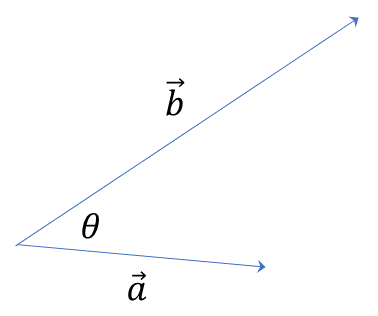
The scalar, or dot, product of two vectors \(\vec{a}\left(a_{1},a_{2},a_{3}\right)\) and \(\vec{b}\left(b_{1},b_{2},b_{3}\right)\) is a scalar, defined by: \[ \vec{a}\cdot\vec{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} \] or geometrically, \[ \vec{a}\cdot\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos\theta \] where \(\theta\) is the angle between \(\vec{a}\) and \(\vec{b}\).
Properties of the Scalar or Dot Product
If \(\vec{a}\) and \(\vec{b}\) are non-zero vectors and \(\vec{a}\) is perpendicular1 Perpendicular means at right angles to. A right angle is \(90^{\circ}=\pi/2.\) to \(\vec{b}\) then \(\vec{a}\cdot\vec{b}=0,\) since \(\cos\left(\frac{\pi}{2}\right)=0\).
If \(\vec{a}\) is parallel to \(\vec{b}\) then the angle between the vectors is \(0\) and \(\vec{a}\cdot\vec{b}=\mid\vec{a}\mid\mid\vec{b}\mid\) as \(\cos\left(0\right)=1\).
The dot product does not depend on the order of multiplication: \[ \vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a} \]
In three dimensions with \(\hat{i},\) \(\hat{j}\) and \(\hat{k}\) unit vectors along the \(x\), \(y\) and \(z\) axes respectively, we have: \[\begin{align*} \vec{i}\cdot\vec{j} & =\vec{j}\cdot\vec{k}=\vec{k}\cdot\vec{i}=0\\ \vec{i}\cdot\vec{i} & =\vec{j}\cdot\vec{j}=\vec{k}\cdot\vec{k}=1 \end{align*}\]
Examples
\(\left(2\vec{i}+3\vec{j}+4\vec{k}\right)\cdot\left(-\vec{i}-2\vec{j}+\vec{k}\right)=\left(2\times\left(-1\right)\right)+\left(3\times\left(-2\right)\right)+\left(4\times1\right)=-4\)
\(\left(2,-3,-3\right)\cdot\left(1,1,-2\right)=2-3+6=5\)
\(\left(5,0,-1\right)\cdot\left(1,4,3\right)=5+0-3=2\)
\(\left(2\vec{i}+4\vec{k}\right)\cdot\left(-3\vec{i}-2\vec{j}\right)=2\times\left(-3\right)+0\times\left(-2\right)+4\times0=-6\)
See Exercises 1, 2, and 3.
Angle Between Two Vectors
The angle \(\theta,\left(0\leq\theta\leq\pi\right)\), between two vectors can be found using the definition of the dot product: \[\begin{align*} \vec{a}\cdot\vec{b} & =\mid\vec{a}\mid\mid\vec{b}\mid\cos\theta. \end{align*}\] Rearranging, \[\begin{align*} \cos\theta & =\frac{\vec{a}\cdot\vec{b}}{\mid\vec{a}\mid\mid\vec{b}\mid} \end{align*}\] and \[\begin{align*} \theta & =\cos^{-1}\left(\frac{\vec{a}\cdot\vec{b}}{\mid\vec{a}\mid\mid\vec{b}\mid}\right). \end{align*}\]
Examples
If \(\vec{a}=\left(2,3,1\right)\) and \(\vec{b}=\left(5,-2,2\right)\) find the angle \(\theta\), between \(\vec{a}\) and \(\vec{b}\) \[\begin{align*} \theta & =\cos^{-1}\left(\frac{\vec{a}\cdot\vec{b}}{\mid\vec{a}\mid\mid\vec{b}\mid}\right)\\ \vec{a}\cdot\vec{b} & =\left(2,3,1\right)\cdot\left(5,-2,2\right)=6\\ \mid\vec{a}\mid & =\sqrt{2^{2}+3^{2}+1^{2}}=\sqrt{14},\mid\vec{b}\mid=\sqrt{25+4+4}=\sqrt{33}\\ \theta & =\cos^{-1}\left(\frac{6}{\sqrt{33}\times\sqrt{14}}\right)\\ & =\cos^{-1}\left(0.2791\right)\\ \theta & =73.8^{\circ}. \end{align*}\] The angle between \(\vec{a}\) and \(\vec{b}\) is \(73.8^{\circ}\).
Find the angle \(\theta\), between \(\vec{a}\left(1,0,1\right)\) and \(\vec{b}\left(-2,-1,1\right).\) \[\begin{align*} \vec{a}\cdot\vec{b} & =\left(1,0,1\right)\cdot\left(-2,-1,1\right)=-1\\ \mid\vec{a}\mid & =\sqrt{2}\\ \mid\vec{b}\mid & =\sqrt{6}\\ \theta & =\cos^{-1}\left(\frac{\vec{a}\cdot\vec{b}}{\mid\vec{a}\mid\mid\vec{b}\mid}\right)=\cos^{-1}\left(\frac{-1}{\sqrt{2}\times\sqrt{6}}\right)=\cos^{-1}\left(-0.2887\right)\\ \theta & =106.8^{\circ}. \end{align*}\]
The angle between \(\vec{a}\) and \(\vec{b}\) is \(106.8^{\circ}\).
See Exercises 4 and 5.
Exercise 1
Calculate the dot product of:
\(\text{(a) $\left(2,5,-1\right)$ and $\left(4,1,1\right)$ }\)
\(\text{(b) $3\vec{i}$ }\) and \(5\vec{j}\)
\(\text{(c)}\) \(5\vec{k}\) and \(\left(\vec{j}+2\vec{k}\right)\)
\(\text{(a) 12}\quad\text{(b) $0\quad\text{(c) $10$ }$ }\)
Exercise 2
Find:
\(\text{(a)$\,\left(2,0,4\right)\cdot\left(-3,1,3\right)$ }\)
\(\text{(b)$\,\left(0,5,1\right)\cdot\left(4,0,0\right)$ }\)
\(\text{(c)$\,\left(2\vec{i}+3\vec{k}\right)\cdot\left(7\vec{i}+2\vec{j}+4\vec{k}\right)$ }\)
\(\text{(a) 6}\quad\text{(b) $0\quad\text{(c) $26$ }$ }\)
Exercise 3
Which of the following vectors are perpendicular?
\(\text{(a)}\,\left(5,2,3\right)\)
\(\text{(b)}\,\left(0,1,-1\right)\)
\(\text{(c)}\,\left(-2,2,2\right)\)
\(\text{(a) and (c), (b) and (c)}\)
Exercise 4
Find the angle between the following pairs of vectors:
\(\text{(a)}\,\left(1,2,3\right)\ \)and \(\left(4,-1,0\right)\)
\(\text{(b)}\,\left(2,1,-2\right)\ \)and \(\left(1,5,-1\right)\)
\(\text{(c)}\,\left(0,5,1\right)\ \)and \(\left(2,0,0\right)\)
\(\text{(d)}\,\left(1,-2,3\right)\ \)and \(\left(-4,1,-3\right)\)
\(\text{(e)}\,\left(2,1,-2\right)\ \)and \(\left(0,4,0\right)\)
\(\text{(f)}\,\left(0,3,0\right)\ \)and \(\left(0,1,0\right)\)
\(\text{(a)$\,82.6^{\circ}\quad\text{(b)$\,54.7^{\circ}\quad\text{(c)$\,90^{\circ}\quad\text{(d)$\,141.8^{\circ}\quad\text{(e)$\,$ $70.5^{\circ}\quad\text{(f)$\,0^{\circ}$ }$ }$ }$ }$ }$ }\)
Exercise 5
If \(\vec{a}=\left(2,2,2\right),\,\vec{b}=\left(3,2,-1\right),\) and \(\vec{c}=\left(-1,4,1\right),\)
\(\text{(a)$\,$ }\)Show \(\vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}\)
\(\text{(b)$\,$ }\)Rearranging \(\vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}\) gives \(\vec{a}\cdot\left(\vec{b}-\vec{c}\right)=0\). As \(\vec{b}\neq\vec{c}\) what is the relationship between \(\vec{a}\) and \(\left(\vec{b}-\vec{c}\right)\)?
\(\text{(a)$\,\vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}=8\quad\text{$(b)$ $\vec{a}$ is perpendicular to $\left(\vec{b}-\vec{c}\right).$ }$ }\)
Download this page, V3 Scalar Product (PDF 173 KB)
What's next... V4 Vector product
