V11 Directional derivatives
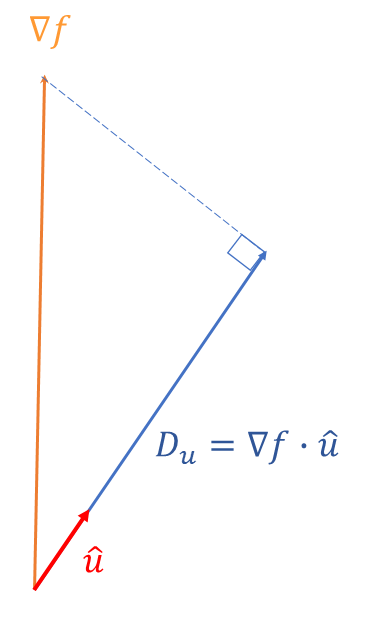
If you are on the side of a hill, the gradient depends on the direction you look. So the directional derivative is the gradient in a particular direction.
(See also Linear graphs)
Learn how to find the directional derivative of a function of two variables f(x,y) or three variables g(x,y,z) at a point and in a given direction. This is very useful in engineering and especially computer graphics.
You will recall that the derivative of a function gives us the gradient or rate of change of the function. The rate of change of a function such as \(z=f\left(x,y\right)\) can be found by \(\text{partial}\) differentiation; \(\frac{\partial f}{\partial x}\) gives the rate of change of the function \(f\), with respect to \(x\), that is, the gradient of the graph as we move in the \(x\) direction. Keep in mind that the graph of \(z=f\left(x,y\right)\) is a surface in three dimensional space and \(\frac{\partial f}{\partial y}\) gives the rate of change of \(f\) with respect to \(y\), that is, the gradient of the graph as we move in the \(y\) direction.
Directional Derivatives
We can find the rate of change of a function in any direction (not just in the direction of the \(x-\) axis or \(y-\) axis) by finding the directional derivative.
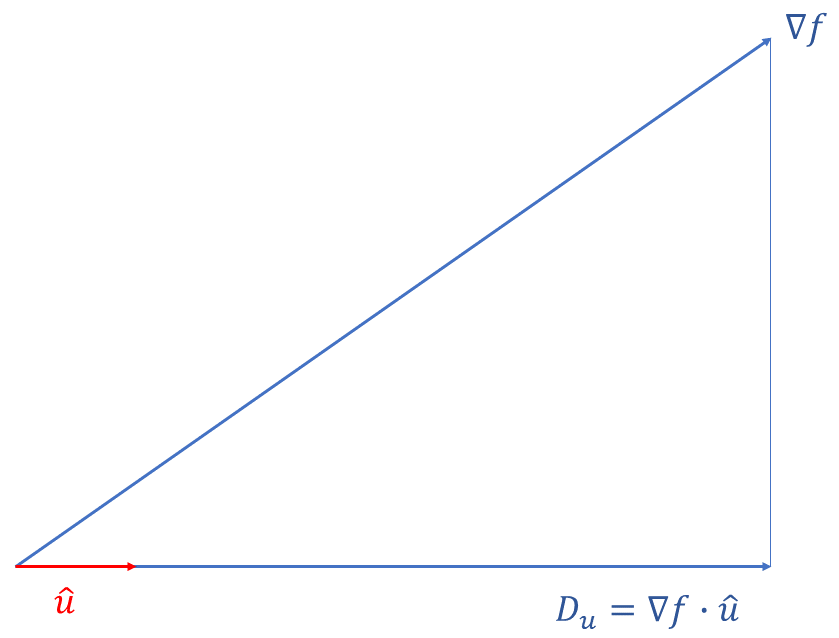
The directional derivative of a function \(f\) in the direction of a vector \(\vec{u}\) is denoted by \(D_{u}\) and is given by:1 Note that the function \(f\) may be of \(2\) or more variables. \[\begin{align*} D_{u} & =\nabla f\cdot\hat{u} \end{align*}\] where \(\hat{u}\) is a unit vector in the direction of the vector \(\vec{u}.\)2 A unit vector is a vector of magnitude \(1.\) For a vector \(\vec{u}\) a unit vector in the direction of \(\vec{u}\) is given by \[\begin{align*} \hat{u} & =\frac{1}{\left|\vec{u}\right|}\vec{u} \end{align*}\] where \(\left|\vec{u}\right|\) is the magnitude of the vector \(\vec{u}\). The following figure illustrates the meaning of the directional derivative:
Example 1
Suppose that we wish to find the directional derivative of \(f\left(x,y\right)=x^{2}+y^{2}\) at the point \(\left(2,3\right)\) in the direction of the vector \(\vec{u}=4\vec{i}-3\vec{j}\).
Solution:
The first step is to find the vector “grad f”, symbolised thus \(\nabla f\).
\[\begin{align*} \nabla f=\frac{\partial f}{\partial x}\vec{i} & +\frac{\partial f}{\partial y}\vec{j}. \end{align*}\]
In this particular case \[\begin{align*} \nabla f & =2x\vec{i}+2y\vec{j}\\ & =4\vec{i}+6\vec{j} \end{align*}\] at the point where \(x=2\) and \(y=3\) .
The next step is to find the dot product of this vector \(\nabla f\), and \(\hat{u}\), the unit vector in the direction of \(\vec{u}\).
In this case \(\vec{u}=4i-3j\), therefore \(\hat{u}=\frac{1}{5}\left(4i-3j\right)\)
Hence the directional derivative of \(f\) in the direction of \(u\) is \[\begin{align*} D_{u} & =\left(4i+6j\right)\cdot\left(\frac{4}{5}i-\frac{3}{5}j\right)\\ & =\frac{16}{5}-\frac{18}{5}\\ & =-\frac{2}{5}. \end{align*}\] To generalise the above, the directional derivative of a function, \(f\), in the direction of \(u\) is \[ D_{u}=\nabla f\cdot\hat{u} \] where \[ \nabla f=\frac{\partial f}{\partial x}i+\frac{\partial f}{\partial y}j+\frac{\partial f}{\partial z}k. \] Since the directional derivative relies on a dot product, (remember \(\vec{a}.\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos\theta\)), it will be a maximum when \(\cos\theta\) is maximum (that is, \(\cos\theta=1\)), so the directional derivative will be maximum when \(\theta=0\).
In other words, we can say that
- \(D_{u}\) will be maximum when \(\vec{u}\) and \(\nabla f\) are in the same direction.
- \(D_{u}\) will have its greatest negative value when \(u\) and \(\nabla f\) are in opposite directions (when \(\theta=\pi\)).
- \(D_{u}\) will be zero when \(u\) and \(\nabla f\) are at right angles.
Example 2
If \(f\left(x,y,z\right)=x^{2}+y^{2}+xyz\), find a unit vector \(\hat{u}\) such that the rate of change of \(f\) at \(\left(2,3,-1\right)\) in the direction of \(u\) is maximum.
Solution: \[\begin{align*} \nabla f= & \frac{\partial f}{\partial x}\hat{i}+\frac{\partial f}{\partial y}\hat{j}+\frac{\partial f}{\partial z}\hat{k}\\ = & \left(2x+yz\right)\hat{i}+\left(2y+xz\right)\hat{j}+\left(xy\right)\hat{k}\\ = & \hat{i}+4\hat{j}+6\hat{k} \end{align*}\]
For the directional derivative to be maximum, \(u=\nabla f\)
Therefore \(u=\hat{i}+4\hat{j}+6\hat{k}\) and \(\hat{u}=\frac{1}{\sqrt{53}}\left(\hat{i}+4\hat{j}+6\hat{k}\right)\).
Exercise
- Find the directional derivative of the given function at the given point in the direction of the indicated vector:
\(\text{a) }\) \(f\left(x,y\right)=xy^{2},\,\left(3,2\right),\,4\hat{i}+3\hat{j}\)
\(\text{b) }\) \(f\left(x,y\right)=e^{xy},\,\left(0,2\right),\,\hat{i}\)
\(\text{c) }\) \(f\left(x,y,z\right)=x^{2}y^{3}z,\,\left(2,-1,3\right),\,\hat{i}-2\hat{j}-2\hat{k}\)
Answers:
\(\text{a) }\) \(\frac{52}{5}\quad\text{b) $2$ $\quad\text{c) $-\frac{76}{3}$ }$ }.\)
- Find the unit vector in the direction in which \(f\) increases most rapidly at \(P\left(1,\pi/2\right)\) for \(f\left(x,y\right)=x^{2}+\cos xy\).
Answer:
\(\hat{u}=0.394\hat{i}-0.919\hat{j}.\)
