V1 Introduction to vectors
The modern idea of vectors appeared late in the 19th century when Josiah Willard Gibbs and Oliver Heaviside (of USA and Britain, respectively) independently developed vector analysis to express the new laws of electromagnetism discovered by the Scottish physicist James Clerk Maxwell.
This page Introduces the basic concepts around vectors (which are measurable quantities with direction such as force). It introduces the concept of a scalar (which is a quantity without a direction such as heat or thermal energy).
It covers vector components (aligned along the horizontal and vertical or the 3-dimensional axes), unit vectors (a vector of size = 1), vector magnitude (or size) and how to add and subtract vectors.
Vectors and Scalars
One example of a vector is velocity . The velocity of an object is determined by the magnitude (speed) and direction of travel. Other examples of vectors are force, displacement and acceleration.
A scalar is a quantity that has magnitude only. Mass, time and volume are all examples of scalar quantities.
Vectors in three-dimensional space are defined by three mutually perpendicular directions and and can be denoted as bold letters or as in this worksheet \(\vec{a}\) or \(\vec{b}\) or \(\vec{c}.\)
A vector in the opposite direction from \(\vec{a}\) is denoted by \(-\vec{a}\).
Vectors can be added or subtracted graphically using the triangle rule.
Adding and Subtracting Vectors
Triangle Rule:
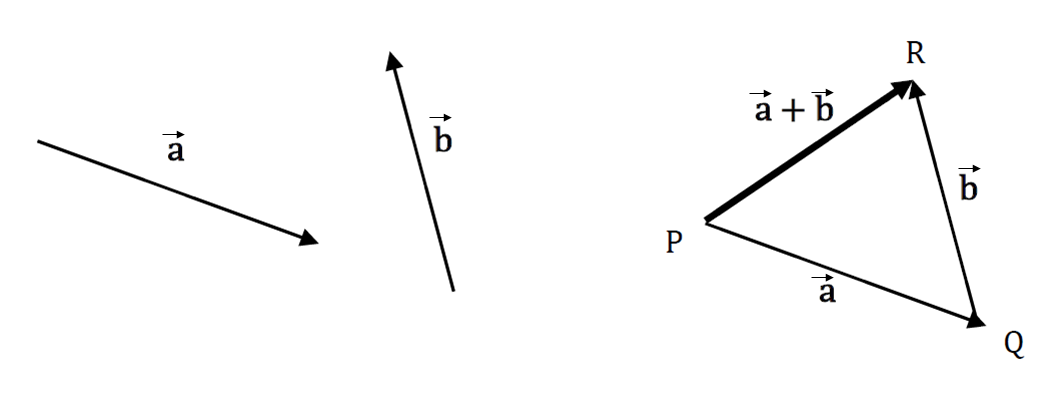
To add vectors \(\vec{a}\) and \(\vec{b}\) shown above place the tail of vector \(\vec{b}\) at the head of vector \(\vec{a}\) (point Q).
The vector sum, \(\vec{a}+\vec{b},\) is the vector \(\overrightarrow{PR}\) , from the tail of vector \(\vec{a}\) to the head of \(\vec{b}.\)
To subtract \(\vec{b}\) from \(\vec{a}\), reverse the direction of \(\vec{b}\) to give \(-\vec{b}\) then add \(\vec{a}\) and \(-\vec{b}\).
\(\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\)
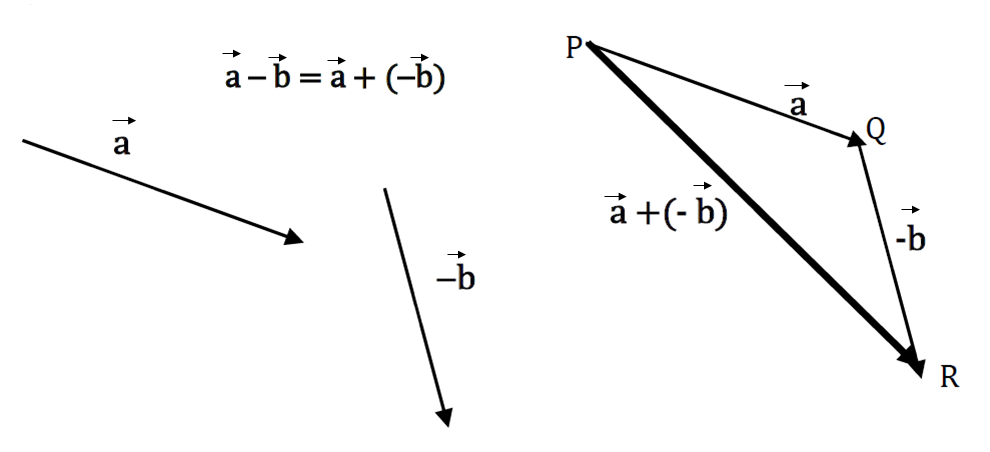
Vector \(\overrightarrow{PR}\) is equal to the vector \(\vec{a}-\vec{b}\).
Components of a Vector
In the diagram below the vector \(\vec{r}\) is represented by \(\overrightarrow{OP}\) where \(P\) is the point \((x,y,z)\).
if \(\vec{i}\) ,\(\vec{j}\) , and \(\vec{k}\) are vectors of magnitude one1 A vector of magnitude one is called a unit vector. Magnitude of vectors and unit vectors are discussed later in this module. parallel to the positive directions of the \(x\)- axis , \(y\)-axis and \(z\)-axis respectively, then:
\(x\vec{i}\) is a vector of length x in the direction of the \(x\)-axis
\(y\vec{i}\) is a vector of length y in the direction of the \(y\)-axis
\(z\vec{k}\) is a vector of length z in the direction of the \(z\)-axis
\(\overrightarrow{OP}\) is then the vector \(x\vec{i}+y\vec{j}+z\vec{k}\)
\(x\), \(y\) and \(z\) are called the components of the vector.
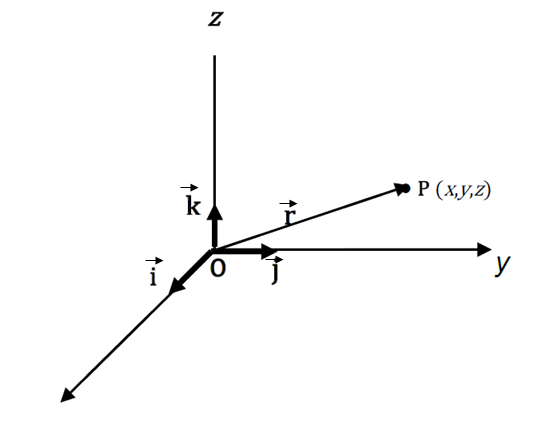
The notation \((x,y,z)\) will be used to denote the vector \(\vec{r}=(x\vec{i}+y\vec{j}+z\vec{k})\) as well as the co-ordinates of a point \(P\) \((x,y,z)\). The context will determine the correct meaning.
Vectors may also be added or subtracted by adding or subtracting their corresponding components.
Example
If \(\vec{a}=(-3,4,2)\) and \(\vec{b}=(-1,-2,3)\) , find:
\[\begin{align*} \vec{a}+\vec{b} & =(-3,4,2)+(-1,-2,3)\\ & =(-3+(-1),4+(-2),2+3)\\ & =(-4,2,5) \end{align*}\] and
\[\begin{align*} \vec{a}-\vec{b} & =(-3,4,2)-(-1,-2,3)\\ & =(-3-(-1),4-(-2),2-3)\\ & =(-2,6,-1) \end{align*}\]
See Exercise 1.
Directed Line Segment
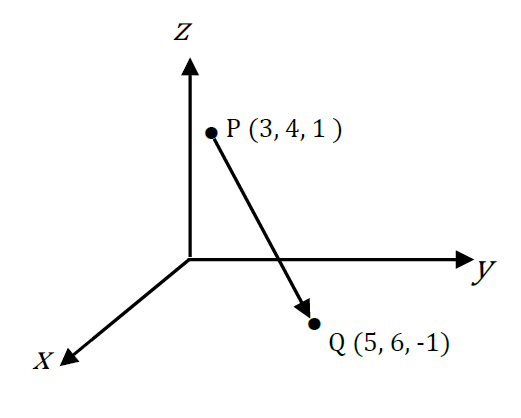
The directed line segment, or geometric vector, \(\overrightarrow{PQ}\) , from\(P(x_{1},y_{1},z_{1})\) to \(Q(x_{2},y_{2},z_{2})\) is found by subtracting the co-ordinates of \(P\) (the initial point) from the co-ordinates of \(Q\) (the final point).
\(\overrightarrow{PQ}=(x_{2}-x_{1})\vec{i}+(y_{2}-y_{1})\vec{j}+(z_{2}-z_{1})\vec{k}\)
Example

\[\begin{align*} \overrightarrow{PQ} & =(5-3)\vec{i}+(6-4)\vec{j}+(-1-1)\vec{k}\\ & =2\vec{i}+2\vec{j}-2\vec{k}. \end{align*}\]
The directed line segment \(\overrightarrow{PQ}\) is represented by the vector \(2\vec{i}+2\vec{j}-2\vec{k}\), or \((2,2,-2)\). Any other directed line segment with the same length and same direction as \(\overrightarrow{PQ}\) is also represented by \(2\vec{i}+2\vec{j}-2\vec{k}\) or \((2,2,-2)\).
The directed line segment \(\overrightarrow{QP}\) has the same length as \(\overrightarrow{PQ}\) but is in the opposite direction.
\[\begin{alignat*}{1} \overrightarrow{QP} & =-\overrightarrow{PQ}\\ & =-(2\vec{i}+2\vec{j}-2\vec{k})\\ & =-2\vec{i}-2\vec{j}+2\vec{k}\\ is\ also\ & =(-2,-2,2) \end{alignat*}\]
Position Vector
The position vector of any point is the directed line segment from the origin \(O\) \((0,0,0)\) to that point and is given by the co-ordinates of of the point.
The position vector of \(P(3,4,1)\) is \(3\vec{i}+4\vec{j}+\vec{k}\), or \((3,4,1)\).
See Exercise 2.
Magnitude of a vector
if \(\vec{a}=a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\) the length or magnitude of \(\vec{a}\) is written as \(\left|\vec{a}\right|\) or \('\vec{a}'\) and is evaluated as:
\(\left|\vec{a}\right|=\sqrt{(a_{1})^{2}+(a_{2})^{2}+(a_{3})^{2}}\)
Example
The length of the vector \(2\vec{i}+3\vec{j}-5\vec{k}\) equals \(\sqrt{2^{2}+3^{2}+(-5)^{2}}=\sqrt{38}\)
In this case \(a_{1}=2,a_{2}=3,a_{3}=-5\)
\(a_{1},a_{2},a_{3}\) are referred to as the components of vector \(\vec{a}\).
Unit Vector
Any vector with a magnitude of one is called a unit vector.
If \(\vec{a}\) is any vector then a unit vector parallel to \(\vec{a}\) is written \(\hat{a}\) (a “hat”). The “hat” symbolises a unit vector.
The unit vector \(\hat{a}\) equals vector \(\vec{a}\) divided by its magnitude \(\left|\vec{a}\right|\) .
\[\begin{alignat*}{1} \hat{a} & =\frac{\vec{a}}{\left|\vec{a}\right|}\\ Rearanging\ & \ gives\\ \vec{a} & =\left|\vec{a}\right|\hat{a} \end{alignat*}\]
Of particular importance are unit vectors \(\vec{i}\), \(\vec{j}\) and \(\vec{k}\), parallel to the \(x\) , \(y\), and \(z\) axes respectively.
Examples
- If \(\overrightarrow{PQ}\) is the line \(2\vec{i}-5\vec{j}+\vec{k}\) find a unit vector parallel to \(\overrightarrow{PQ}\)
\(\overrightarrow{PQ}=\sqrt{2^{2}+\left(-5\right)^{2}+1^{2}}=\sqrt{30}\)
A unit vector parallel to \(\overrightarrow{PQ}\) is :
\[\begin{alignat*}{1} \overrightarrow{PQ} & =\frac{\overrightarrow{PQ}}{\left|\overrightarrow{PQ}\right|}\\ & =\frac{(2\vec{i}-5\vec{j}+\vec{k})}{\sqrt{30}}\\ & =\frac{1}{\sqrt{30}}(2\vec{i}-5\vec{j}+\vec{k}) \end{alignat*}\]
- if \(\vec{a}\) \(=(1,2,3)\) a unit vector parallel to \(\vec{a}\) is:
\[\begin{alignat*}{1} \hat{a} & =\frac{\vec{a}}{\left|\vec{a}\right|}\\ & =\frac{(1i+2j+3k)}{\sqrt{1^{2}+2^{2}+3^{2}}}\\ & =\frac{(1i+2j+3k)}{\sqrt{14}}\\ & =\frac{1}{\sqrt{14}}(1i+2j+3k) \end{alignat*}\]
see Exercise 3.
Multiplication by a Scalar
To multiply a vector \(\vec{a}=\) \(a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\) by a scalar, \(m\), multiply each component of \(\vec{a}\) by \(m\).
\[\begin{alignat*}{1} m\vec{a} & =ma_{1}\vec{i}+ma_{2}\vec{j}+ma_{3}\vec{k} \end{alignat*}\]
The result is a vector of length \(m\times\left|\vec{a}\right|\)
If \(m>0\) the resultant vector is in the same direction as \(\vec{a}\)
If \(m<0\) the resultant vector is in the opposite direction from \(\vec{a}\).
Two vectors a and b are said to be parallel if and only if \(\vec{a}=k\vec{b}\) where \(k\) is a real constant.
Example
Multiply \(\vec{a}=(3\vec{i}+\vec{j}-2\vec{k})\) by \(7\) and show \(\left|7\vec{a}\right|=7\left|\vec{a}\right|\)
\[\begin{alignat*}{1} 7\vec{a} & =7(3\vec{i}+\vec{j}-2\vec{k})\\ & =21\vec{i}+7\vec{j}-14\vec{k}\\ so\ that\\ \left|7\vec{a}\right| & =\sqrt{21^{2}+7^{2}+(-14)^{2}}\\ & =\sqrt{686}=\sqrt{49\times14}\\ & =7\sqrt{14} \end{alignat*}\]
Also the magnitude of \(\vec{a}\) is \[\begin{alignat*}{1} \left|\vec{a}\right| & =\sqrt{3^{2}+1^{2}+(-2)^{2}}=\sqrt{14}\\ 7\left|\vec{a}\right| & =7\sqrt{14} \end{alignat*}\]
Therefore we can derive:
\[\begin{alignat*}{1} \left|7\vec{a}\right| & =7\left|\vec{a}\right|=7\sqrt{14}. \end{alignat*}\]
See Exercise 4.
Exercise 1
Given \(\vec{a}=(2,1,1)\) , \(\vec{b}=(1,3,-3)\) and \(\vec{c}=(0,3,-2)\) find:
- \(\vec{a}+\vec{b}\)
- \(\vec{a}+\vec{c}\)
- \(\vec{c}-\vec{b}\)
- \(\vec{a}-\vec{b}\).
a) \(\left(3,4,-2\right)\quad\) b) \(\left(2,4,-1\right)\quad\) c) \(\left(-1,0,1\right)\quad\) d) \(\left(1,-2,4\right)\)
Exercise 2
- Given the points \(A(3,0,4)\) , \(B(-2,4,3)\), and \(C(1,-5,0)\), find:
\(\text{i}.\;\overrightarrow{AB}\quad\) ii. \(\overrightarrow{AC}\quad\) iii. \(\overrightarrow{CB}\quad\) iv. \(\overrightarrow{BC}\quad\) v. \(\overrightarrow{CA}\)
Compare your answers to (ii) and (v), and also to (iii) and (iv). What do you notice?
- What are the position vectors of the points \(A,\,B\) and \(C\)?
\(\text{a.i)}\) \(\left(-5,4,-1\right)\quad\)ii) \(\left(-2,-5,-4\right)\quad\) iii) \(\left(-3,9,3\right)\quad\) iv) \(\left(3,-9,-3\right)\quad\) v) \(\left(2,5,4\right)\)
They are in opposite directions.
\(\text{b.}\) \(\overrightarrow{OA}=3\vec{i}+4\vec{k}\), \(\overrightarrow{OB}=-2\vec{i}+4\vec{j}+3\vec{k}\)
and \(\overrightarrow{OC}=\vec{i}-5\vec{j}\).
Exercise 3
Find the length of the vectors:
\(\text{(i)}\;(3,-1,-1)\quad\) (ii) \((0,2,4)\quad\) (iii) \((0,-2,0)\)Given the points \(A\,(3,0,4)\), \(B\,(0,4,3)\) and \(C\,(1,-5,0)\);
find unit vectors parallel to \(\text{(i)}\;\overrightarrow{BA}\quad\text{(ii) $\overrightarrow{CB}\quad\text{(iii) $\overrightarrow{AC}$ .}$ }\)
\(\text{a.$\,$ i)$\;$ }\) \(\text{$\sqrt{11}$ $\quad$ }\)ii) \(\sqrt{20}=2\sqrt{5}\quad\) iii) \(2\)
\(\text{b.$\,$ i)$\;$ }\) \(\frac{(3,-4,1)}{\sqrt{26}}\quad\)ii) \(\frac{(-1,9,3)}{\sqrt{91}}\quad\)iii) \(\frac{(-2,-5,-4)}{\sqrt{45}}=\frac{(-2,-5,-4)}{3\sqrt{5}}\)
Exercise 4
Expand the following: (i) \(3(\vec{i}+3\vec{j}-5\vec{k})\) (ii) \(-4(\vec{j}-3\vec{k})\)
If \(\vec{a}=(2,-2,1)\) , \(\vec{b}=(0,1,1)\) and \(\vec{c}=(-1,3,-2)\) , find (i) \((2\vec{a}+3\vec{b})\) (ii) \((3\vec{a}-2\vec{b})\) (iii) \((2\vec{a}-\vec{b}+2\vec{c})\) (iv) a unit vector parallel to \(2\vec{a}-\vec{b}\)
Write down a vector three times the length of \((6\vec{i}+2\vec{j}-5\vec{k})\) and in the opposite direction.
a. i) \(\left(3\vec{i}+9\vec{j}-15\vec{k}\right)\quad\)ii) \(\left(-4\vec{j}+12\vec{k}\right)\)
b. i) \(\left(4,-1,5\right)\quad\)ii) \(\left(6,-8,1\right)\quad\)iii) \(\left(2,1,-3\right)\quad\)iv) \(\frac{(4,-5,1)}{\sqrt{42}}\)
c. \(\left(-18\vec{i}-6\vec{j}+15\vec{k}\right).\)
Download this page, V1 Introduction to vectors (PDF 214KB)
What's next... V2 Resolution of vectors
