T4 Cosine rule

The cosine rule is a generalisation of Pythagoras’ theorem. If you have any two sides of a triangle, as long as you know the angle between them, you can calculate the length of the third side.
The Cosine Rule can be used to solve non-right triangles.
The Cosine Rule
Consider the triangle below:
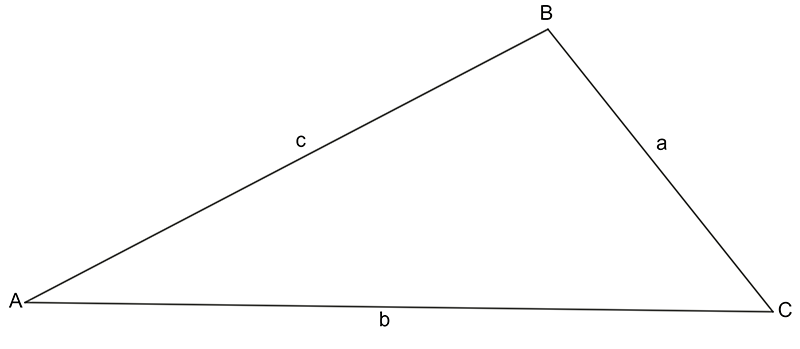
The angles A, B, C are the angles at the vertices A, B, C respectively. The sides a, b, and c are opposite angles A, B, C respectively.
The Cosine Rule states:
\[\begin{align*} a^{2} & =b^{2}+c^{2}-2bc\cos A\\ b^{2} & =a^{2}+c^{2}-2ac\cos B\\ c^{2} & =a^{2}+b^{2}-2ab\cos C. \end{align*}\]
Note that the side on the left hand side of the equation is opposite the angle listed at the end of the equation:
\[\begin{align*} \boldsymbol{\underline{a^{2}}} & =b^{2}+c^{2}-2bc\,\cos\boldsymbol{\underline{A}}. \end{align*}\]
Use the Cosine Rule when you are given:
two sides and the angle between them, or
all three sides of the triangle.
Examples
- Find the value of \(a\) in this triangle

\[\begin{align*} a^{2} & =b^{2}+c^{2}-2bc\,\cos A\\ a^{2} & =12^{2}+15^{2}-2\times12\times15\times\cos83^{\circ}\\ a^{2} & =144+225-360\times\cos83^{\circ}\\ a^{2} & =369-43.87\\ a^{2} & =325.13\\ a & =18.03 \end{align*}\]
- Find the size of angle B in this triangle:
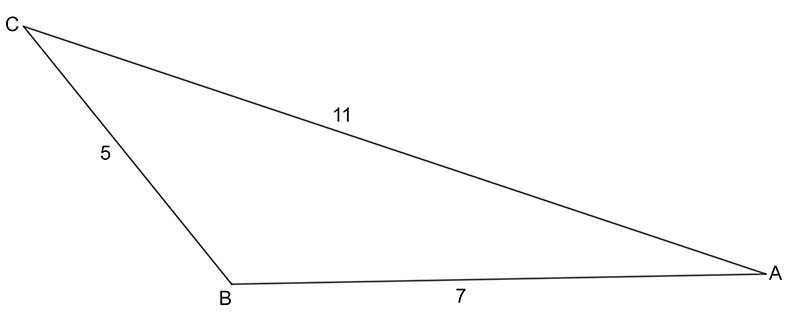
\[\begin{align*} b^{2} & =a^{2}+c^{2}-2ac\,\cos B\\ 11^{2} & =5^{2}+7^{2}-2\times5\times7\times\cos B\\ 121 & =25+49-70\times\cos B\\ 121-25-49 & =-70\times\cos B\\ 47 & =-70\times\cos B\\ \frac{47}{-70} & =\cos B\\ B & =\cos^{-1}\left(-\frac{47}{70}\right)\\ B & =132^{\circ}11^{\prime} \end{align*}\]
Exercise
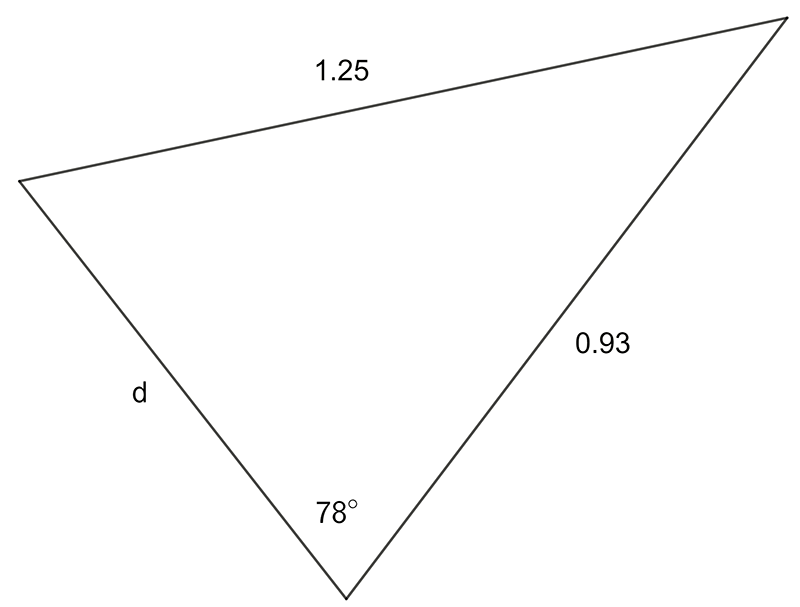
- Use the sine OR cosine rule to find the pro-numeral shown:

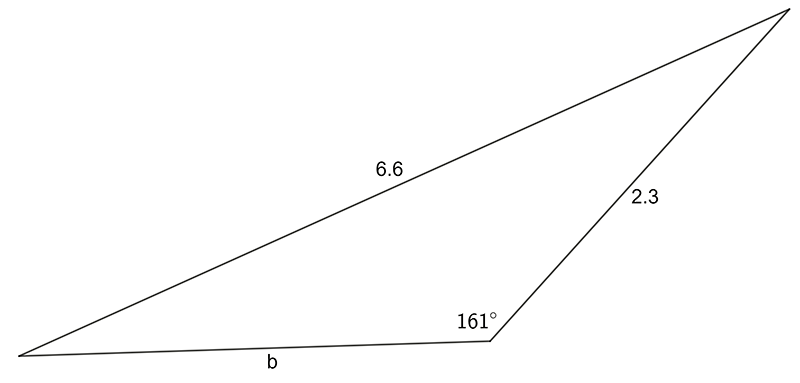
c)
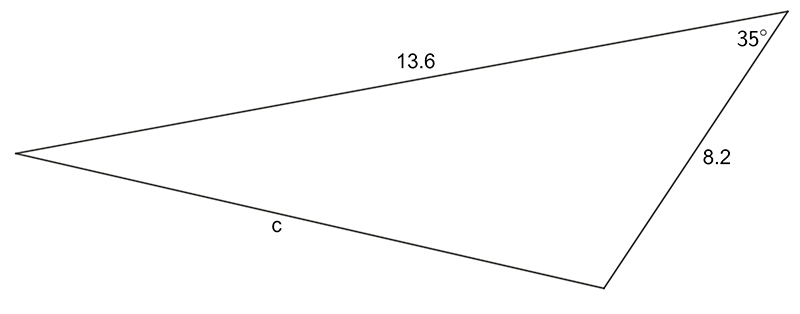
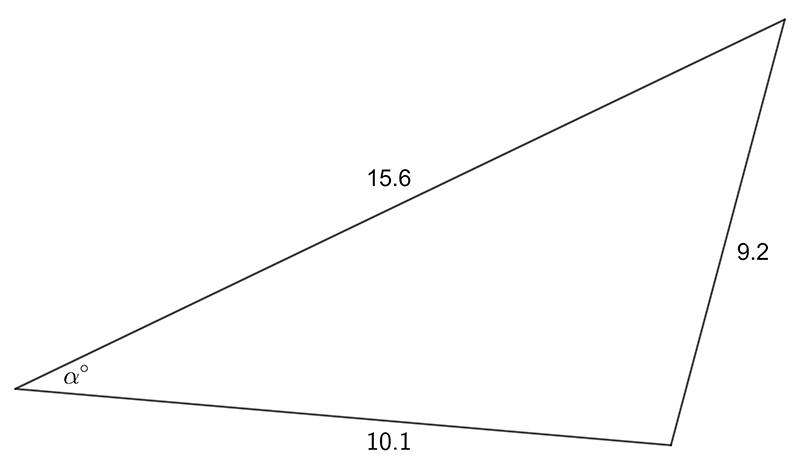
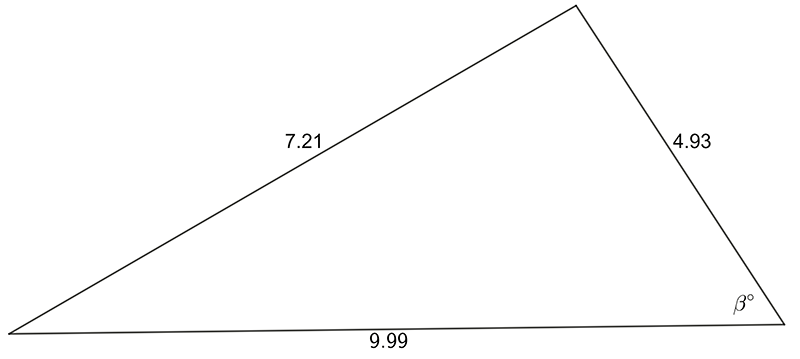
- Find the magnitude of the labeled, unknown angle
1 a) \(28.7\quad\) b) \(4.38\quad\) c) \(8.33\quad\)d) \(1.05\)
2 a) \(\alpha=34.2^{\circ}\quad\) b) \(\beta=42.9^{\circ}.\)
Download this page, T4 Cosine rule (PDF 718KB)
What's next... T5 Angular measurement and the unit circle
