S1 Summation notation
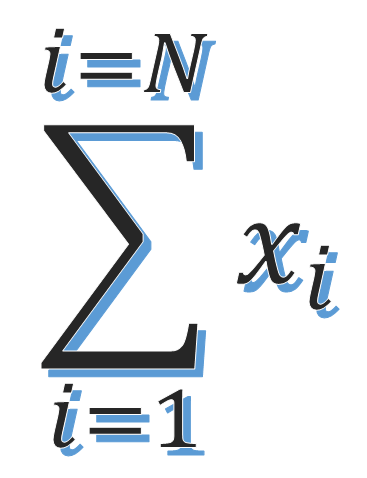
Summation notation or sigma notation is a shorthand method of writing the sum or addition of a string of similar terms. This module explains the use of this notation.
The Basic Idea
We use the Greek symbol sigma \(\Sigma\) to denote summation. \(\Sigma\) is called the summation sign.
A typical element of the sequence which is being summed appears to the right of the summation sign as shown in the figure below:
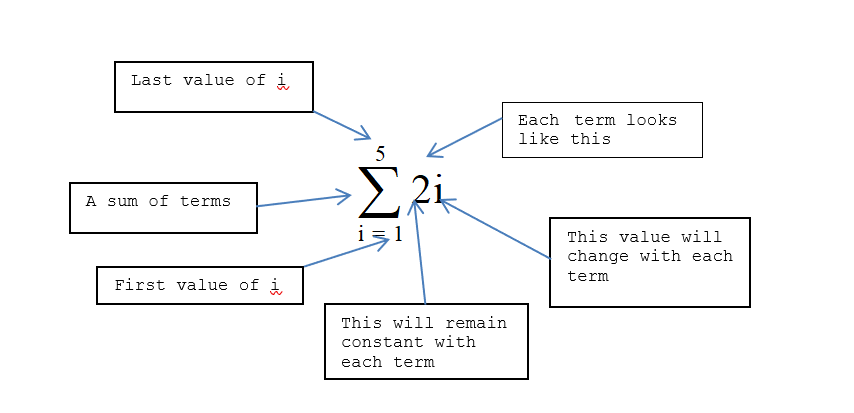
This is written as \({\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}2i\).
To expand and work out it’s value, we replace \(i\) by its starting value (below the sigma symbol) and obtain each successive term by adding \(1\) to the previous value until we reach the final value of \(i\) (above the sigma symbol) and then we evaluate.
For the above sequence: \[\begin{align*} {\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}2i & =2\times1+2\times2+2\times3+2\times4+2\times5=30\\ & =2+4+6+8+10\\ & =30. \end{align*}\]
Example
Expand and evaluate \({\textstyle \mathop{{\textstyle \sum_{i=0}^{3}}}}(i^{2}-3)\)
Note that only the \(i\) value changes in each term.
\[\begin{align*} {\textstyle \mathop{{\textstyle \sum_{i=0}^{3}}}}(i^{2}-3) & =\underbrace{(0^{2}-3)}_{i=0}+\underbrace{(1^{2}-3)}_{i=1}+\underbrace{(2^{2}-3)}_{i=2}+\underbrace{(3^{2}-3)}_{i=3}\\ & =(-3)+(-2)+1+6\\ & =2. \end{align*}\]
Data Sets
Subscripted variables are used to indicate values in a data set. \(x_{1},x_{2},x_{3}...\) refers to first value, second value, third value and so on. Formulae used to calculate summary measures of a data set make use of summation notation.
Example
Given the set of data \(x_{1}=1,x_{2}=2,x_{3}=4,x_{4}=5\) evaluate
- \(\overline{x}=\frac{{\textstyle \mathop{{\textstyle \sum_{i=1}^{n}x_{i}}}}}{n}\) where \(n\) is the number of items in the data set
This formula calculates the mean or average of a set of data.
\[\begin{align*} \overline{x} & =\frac{{\textstyle \mathop{{\textstyle \sum_{i=1}^{4}x_{i}}}}}{4}\\ & =\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}\\ & =\frac{1+2+4+5}{4}\\ & =3 \end{align*}\]
- \(s^{2}=\) \(\frac{{\textstyle \mathop{{\textstyle \sum_{i=1}^{4}(x_{i}-}\overline{x})^{2}}}}{n-1}\)
This formula calculates the variance (a measure of spread around the mean) of a sample of data.
\[\begin{align*} s^{2} & =\frac{{\textstyle \mathop{{\textstyle \sum_{i=1}^{4}(x_{i}-}\overline{x})^{2}}}}{n-1}\\ & =\frac{{\textstyle \mathop{{\textstyle (x_{1}-}\overline{x})^{2}}}+{\textstyle \mathop{{\textstyle (x_{2}-}\overline{x})^{2}}}+{\textstyle \mathop{{\textstyle (x_{3}-}\overline{x})^{2}}}+{\textstyle \mathop{{\textstyle (x_{4}-}\overline{x})^{2}}}}{3}\\ & =\frac{{\textstyle \mathop{{\textstyle (1-}3)^{2}}}+{\textstyle \mathop{{\textstyle (2-}3)^{2}}}+{\textstyle \mathop{{\textstyle (4-}3)^{2}}}+{\textstyle \mathop{{\textstyle (5-}3)^{2}}}}{3}\\ & =\frac{4+1+1+4}{3}\\ & =\frac{10}{3}. \end{align*}\]
Exercise 1
Find
\({\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}3i\)
\({\textstyle \mathop{{\textstyle \sum_{i=1}^{3}}}}(5i-2)\)
\({\textstyle \mathop{{\textstyle \sum_{i=1}^{3}}}(}5i)-2\)
- \(45\;\) b. \(24\;\) c. 28
Exercise 2
Given \(x_{1}=-2,\,x_{2}=0,\,x_{3}=1,\,x_{4}=3,\,x_{5}=3\) evaluate
\({\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}10x_{i}\)
\({\textstyle \mathop{{\textstyle 10\sum_{i=1}^{5}}}}x_{i}\)
\({\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}(x_{i})^{2}\)
\(\left({\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}x_{i}\right)\) \(^{2}\)
\({\textstyle \mathop{{\textstyle \sum_{i=1}^{5}}}}i\times(x_{i})\)
\(\overline{x}=\frac{{\textstyle \mathop{{\textstyle \sum_{i=1}^{n}x_{i}}}}}{n}\)
- \(50\;\) b. \(50\;\) c. \(23\)
\(\qquad\quad\)d. \(25\;\) e. \(28\;\) f. \(1\)
Download this page, S1 Summation notation (PDF 139KB)
What's next... S2 Data
