PV1.1 Addition of vectors
Many concepts in physics may be represented by vectors. A vector has both a size (called its magnitude) and a direction. This module explains how vectors may be added together.
Scalars and Vectors
Many physical quantities can be classified into one of two groups: scalars or vectors.
Scalar quantities are completely defined by a magnitude and the relevant unit. For example, a time period may be expressed as 10 seconds. The magnitude is 10, the unit is seconds and there is no direction associated with a time period, so time is a scalar quantity.
Vector quantities require magnitude and direction and the relevant unit. For example, suppose I walk in a Northerly direction for 200 metres. The magnitude is 200, the direction is North and the unit is metres. So my walk is a vector quantity.
Examples
Some examples of vector and scalar quantities are shown below:
| Physical Quantity | Scalar | Vector | Example of Unit |
|---|---|---|---|
| time | \(\checkmark\) | \(\times\) | seconds, hours, days, etc. |
| distance | \(\checkmark\) | \(\times\) | centimeters, metres, kilometres etc. |
| displacement | \(\times\) | \(\checkmark\) | 100 metres North, 50 metres in the \(x\)-direction |
| temperature | \(\checkmark\) | \(\times\) | \(45^{\circ}\) Celsius |
| speed | \(\checkmark\) | \(\times\) | 100 kilometres per hour, 3 metres per second |
| velocity | \(\times\) | \(\checkmark\) | 100 kilometres per hour, South; 3 \(ms^{-1}\) parallel to the \(y-\)axis |
| voltage | \(\checkmark\) | \(\times\) | 250 millivolts DC |
Representing Vector Quantities
Vectors are drawn by an arrow, whose length varies with the magnitude of the vector (drawn to scale!) and which points in the appropriate direction. For example, suppose North is up the page, South is down, East is to the right and West is to the left. \(A\) vector from a point \(A\) to a point \(B\) (East of \(A\)) representing a distance of 10 metres could be shown as in the diagram below1 We call \(A\) the tail of the vector and \(B\) the head of the vector., East is assumed to be positive so the arrow points towards \(B\).

Using the same scale, a vector representing a distance of 2 metres to the west of A could be represented by:

The beginning and end of a vector may be identified by letters such as \(A\) and \(B\) as above. In such cases the vector may be referred to as \(\overrightarrow{AB\,\,}\). The arrow above the letters signifies that the quantity \(AB\) is a vector but does not point in the direction of the vector.
If we wanted a vector of magnitude 10 meters pointing West it would look like:

This vector is referred to as \(\overrightarrow{BA\,\,}.\) Note that \[ \overrightarrow{AB\,\,}=-\overrightarrow{BA\,\,}. \] In other words, multiplying a vector by \(-1\) changes the direction of the vector.
Magnitude of a Vector
Sometimes we want to use only the magnitude (size) of a particular vector. In such cases, to distinguish that it is only the magnitude that is being used, we use the modulus sign \(\left|\right|\). So for the vector \(\overrightarrow{AB\,\,}\) above we would have \[ \left|\overrightarrow{AB\,\,}\right|=10\textrm{ metres} \] as \(\overrightarrow{AB\,}\) represented a distance of 10 metres to the East.
Examples
The magnitude of a vector representing a velocity of 30 \(\textrm{ms}^{-1}\)in a southerly direction is 30 \(\textrm{ms}^{-1}\).
The magnitude of a force of 18 Newtons in a Westerly direction is 18 Newtons.
Adding Vectors
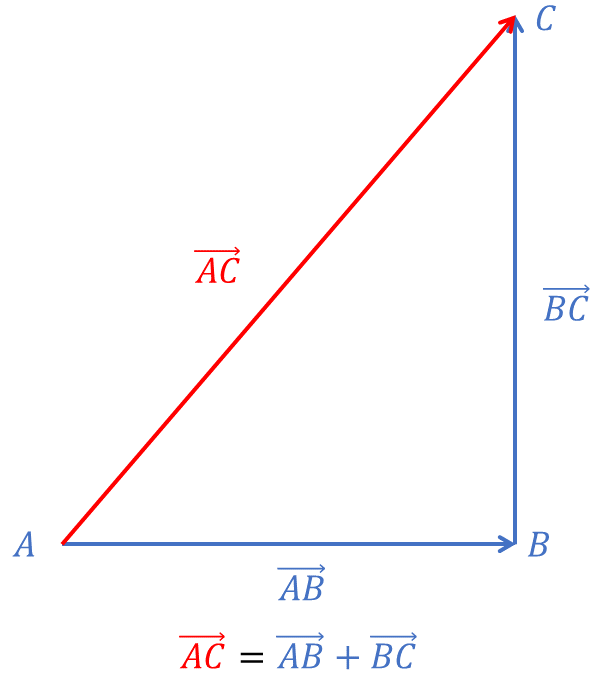
Two vectors are added by placing the tail of the second vector at the head off the first and drawing an arrow from the tail of the first to the head of the second. For example we will add a vector that is 2 metres to the east to another vector that is 5 metres to the east. The two vectors to be added together are shown in red and the resulting vector is shown in blue.

We can write this algebraically as: \[ \overrightarrow{AB\,\,}+\overrightarrow{CD\,\,}=\overrightarrow{AD\,\,}. \] The vector \(\overrightarrow{AD\,\,}\) is called the resultant and in this case is a vector of magnitude 7 metres in an Easterly direction.
We can also add vectors that are in North and South directions. For example if we add a vector representing 2 metres South to a vector representing 4 meters North we get:
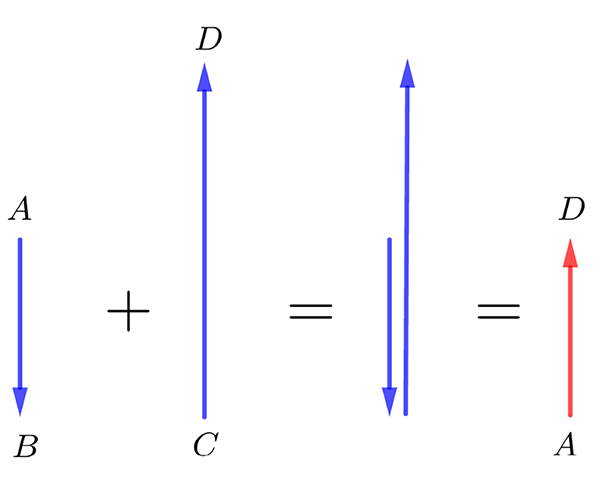
Notice that the vector to the South is shown pointing downwards as we assume North is up. The result is a vector (shown in red) of length 2 meters pointing North. We could write this as
\[ \overrightarrow{AB\,\,}+\overrightarrow{CD\,\,}=\overrightarrow{AD\,\,} \] as before.
Now add a vector of 3 meters to the North to another of 4 meters to the East:
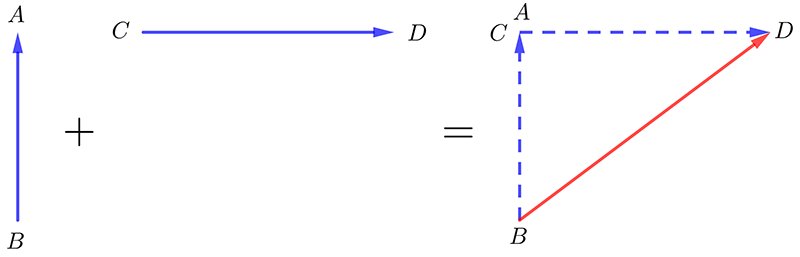
The resultant vector \(\overrightarrow{BD\,\,}\) is shown in red. It’s magnitude may be found using Pythagoras’s Theorem:2 Note that the angle \(\widehat{BCD}\) or \(\widehat{BAD}\) is 90 degrees and so Pythagoras’s Theorem can be used. \[\begin{align*} \left|\overrightarrow{BD\,\,}\right| & =\sqrt{\left|\overrightarrow{BA\,\,}\right|^{2}+\left|\overrightarrow{CD\,\,}\right|^{2}}\\ & =\sqrt{3^{2}+4^{2}}\\ & =\sqrt{9+16}\\ & =\sqrt{25}\\ & =5. \end{align*}\] The direction my be found by calculating the angle \(\widehat{CBD}\). That is \[\begin{align*} \widehat{CBD} & =\tan^{-1}\left(\frac{\left|\overrightarrow{CD\,\,}\right|}{\left|\overrightarrow{AB\,\,}\right|}\right)\\ & =\tan^{-1}\left(\frac{4}{3}\right)\\ & =53.13^{\circ}. \end{align*}\] So the resultant vector has a magnitude of 5 metres in a direction North \(53.13\) degrees East.
Exercises
1.(a) To \(\overrightarrow{60\,\,}\)km East, add \(\overrightarrow{25\,\,}\)km East\(\quad\)(b) To \(\overrightarrow{60\,\,}\)km East, add \(\overrightarrow{25\,\,}\)km West.
2.(a) To \(\overrightarrow{30\,\,}\)km West, add \(\overrightarrow{40\,\,}\)km North\(\quad\)(b) To \(\overrightarrow{30\,\,}\)km West, add \(\overrightarrow{30\,\,}\)km South.
3. A ship sails \(\overrightarrow{40\,\,}\)km North East, add then changes direction and sails \(\overrightarrow{40\,\,}\)km South East. Find the displacement of the ship.
4. Two forces \(\overrightarrow{100\,\,}\) Newtons North and \(\overrightarrow{100\,\,}\) Newtons East are acting away from the same point. Find their vector sum (also called the resultant force).
5. A plane is flying due North at 300 km/h and a Westerly wind of 25 km/h is blowing it off course. Calculate the true speed and the direction of the plane.
1.(a) 85 km East\(\quad\)(b) 35 km East.
2.(a) 50 km North \(37^{\circ}\) West (or \(323^{\circ}\)True)\(\quad\)(b) 42 km South West or (or \(225^{\circ}\) True).
3. 56 km East.
4. 141 Newtons North East.
5. 301 km/h North \(5^{\circ}\) East (or \(005^{\circ}\) True).
