PF1.2 Forces on Slopes
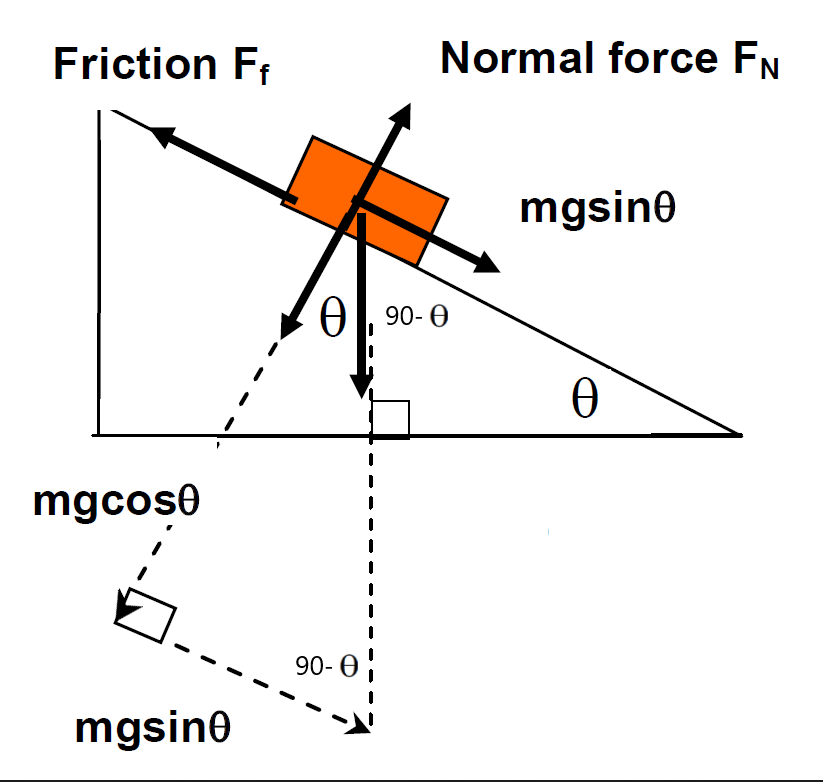
Forces on object sliding downhill
We will look at the gravitational force acting on an object on a slope. These can be divided into two components, the normal (resisting) force pushing into the slope which produces friction and the shear or driving force pushing the block down the slope. So we must consider forces parallel and perpendicular to the slope.
Diagrams of forces acting on an inclined plane
Just as we can analyse the horizontal and vertical components of the motion of an object separately, we can look at components parallel to, and perpendicular to, the sloping surface as well. The normal force of an object placed on a sloping surface is always perpendicular to the surface and the other forces are parallel to the surface. See diagrams below.
Forces acting on a block on an inclined plane:
(At rest or slipping down the plane.)
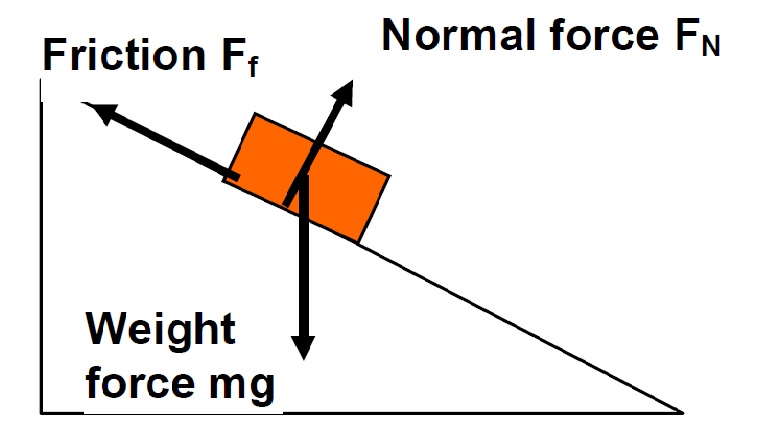
Weight Force acting on a block resolved into its components:
Perpendicular and parallel to the incline. Remember that the normal force \(F_{N}\) is equal and opposite to the force exerted by the object on the plane \(mg\cos\theta\) (perpendicular to plane) otherwise it would fall through the plane, and \(mg\sin\theta\) (parallel to plane) forcing the object down the plane if no friction occurs.

To work out the angles remember sum of angles in any triangle is 180 degrees and remember a right angle is 90 degrees.
Note that with the above diagrams:
Weight \(=mg\); acts through the centre of mass.
Normal force \(F_{N}\) is always at right angles to the surface.
Friction acts to oppose sliding motion (eg, if the mass were being dragged uphill, friction would act downhill)
The weight force is resolved into 2 components:
\(\ \ (1)\ \ \) perpendicular to plane, and
\(\ \ (2)\ \ \) parallel to the plane.
The resultant force \(\Sigma F\) down the slope is given by \(\Sigma F=mg\sin\theta-F_{f}\) where \(F_{f}\) is friction
The resultant force \(\Sigma F\) perpendicular to the slope is zero (because it sits on the slope), hence: \(mg\cos\theta=F_{N}\)
Example:
A toy car of mass \(50g\) travels down a smooth incline at \(30\) degrees to the horizontal. Calculate:
\(\ \ \ \ \)The net force acting on the car as it rolls down the slope, and
\(\ \ \ \ \)The force of the incline on the car as it travels down the slope.
Friction may be ignored in this case. Gravity = 9.8\(ms^{-2}\).
Forces parallel to slope:
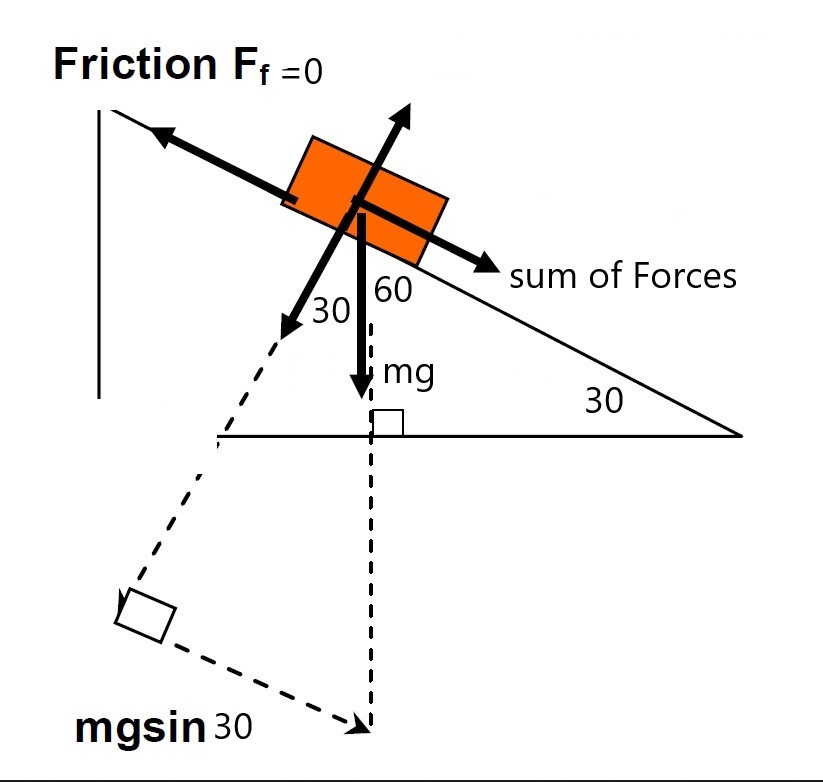
Note the angles: If slope is \(30\) degrees then \(90-30=60\) degrees in top corner then again \(90-60=30\) degrees from normal to vertical force so we would use \(mg\sin30\) down the slope as the sum of all forces.
(a)\(\ \ \ \ \ \) As \(mg\sin\theta\) is the component of the force parallel to the slope then “sum of all forces” = \(\Sigma F\):
\[\begin{align*} \Sigma F & =ma\\ & =mg\sin\theta-F_{f}\\ & =mg\sin\theta-0\\ & =mg\sin\theta \end{align*}\]
Where \(mg\sin\theta\) is the component of the force parallel to the slope.
Note: the surface is friction-less (smooth) ie. \(F_{f}=0\), therefore the only force allowing the car to roll down the incline is the component of the gravitational force ‘\(mg\sin\theta\)’ .
\[\begin{align*} \Sigma F & =mg\sin\theta\\ & =m\times g\times\sin\theta\\ & =50\times10^{-3}\times9.8\times\sin30\\ & =0.25N \end{align*}\]
Note: grams have been converted into kilograms
Forces perpendicular to slope:
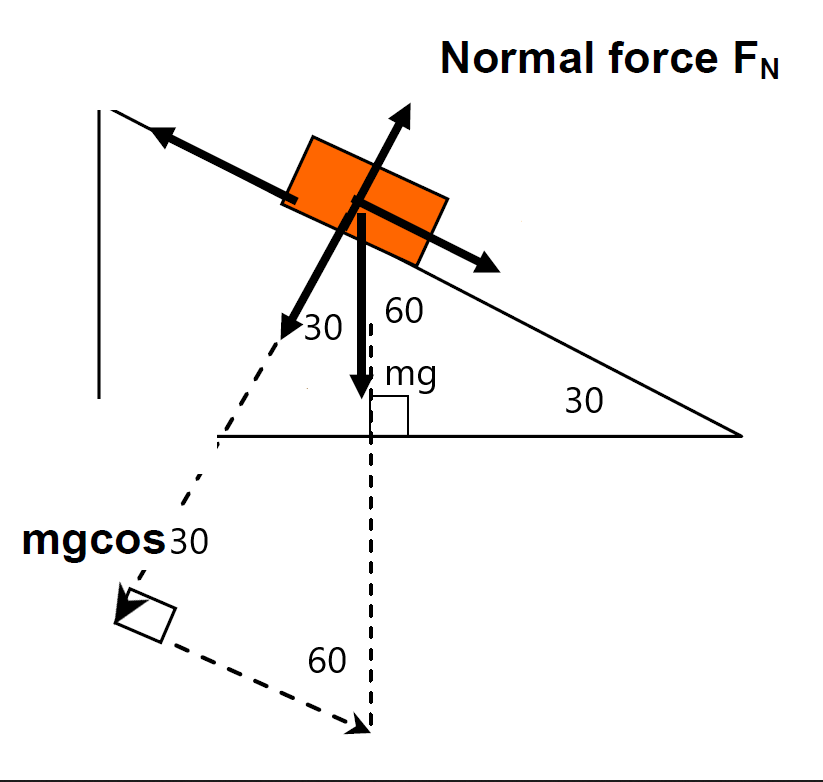
Also note the angles: If slope is \(30\) degrees then \(90-30=60\) degrees in top corner then again \(90-60=30\) degrees from normal to vertical force so we use \(mg\cos30\) perpendicular to the slope as the normal force.
(b)\(\ \ \ \ \ \) The force of the incline on the car is a force that acts perpendicular to the slope, ie. the normal force \(F_{N}\) is equal to \(mg\cos\theta\)
\[\begin{align*} F_{N} & =mg\cos\theta\\ & =m\times g\times\cos\theta\\ & =50\times10^{-3}\times9.8\times\cos30\\ & =0.43N \end{align*}\]
Trivia
The steepest road in the world is in Dunedin, New Zealand. It has an incline of \(52\) degrees. Ignoring friction, a car left with its handbrake off would accelerate down this street at:
\[\begin{align*} a & =g\times\sin\theta\\ & =9.8\times\sin52\\ & =7.7ms^{-2} \end{align*}\]
Hint: always draw the diagram of what is happening. The force along the slope is \(mg\sin\theta\) so \(\Sigma F=ma=mg\sin\theta\) since there is no frictional force.
Exercise
- A skateboarder riding a skateboard of total mass \(60kg\) coasts down a friction-less ramp at an angle of \(30\) degrees to the horizontal. Remember \(g=9.8ms^{-2}\).
\(\ \ \ \ \)Calculate the normal force acting on the rider and skateboard.
\(\ \ \ \ \)Calculate the force acting on the rider and skateboard parallel to the ramp.
- The skateboarder now coasts down another ramp, but this time the ramp has a rough surface.
\(\ \ \ \ \)Calculate the normal force acting on the rider and skateboard
\(\ \ \ \ \)Calculate the force acting on the rider and skateboard parallel to the ramp.
\(\ \ \ \ \)If the ramp has a frictional force of \(54N\), what is the net force acting on the rider and the skateboard?
\(\ \ \ \ \)Calculate the acceleration of the skateboarder.
\(\ \ \ \ \)If the skateboarder started from rest, and the ramp is \(4m\) long, what was the speed of the skateboarder at the bottom of the ramp?
- \(509N\) b. \(294N\)
- \(509N\) b. \(294N\) c.\(240N\) d.\(4ms^{-2}\) e. \(5.7ms^{-1}\) .
