NM3 The trapezoidal rule
You will have evaluated definite integrals such as \[\begin{align*} \int_{1}^{3} & \left(x^{2}\right)dx \end{align*}\] before. In doing this, you are evaluating the area under the graph of \(f\left(x\right)=x^{2}\) between \(x=1\) and \(x=3.\) This is only possible if you can find an antiderivative for \(x^{2}\). In this example it is easy, the antiderivative is \[\begin{align*} F\left(x\right) & =\frac{1}{3}x^{3}+c,\text{ where $c$ is a constant.} \end{align*}\] and \[\begin{align*} \int_{1}^{3}\left(x^{2}\right)dx & =F\left(3\right)-F\left(1\right)\\ & =\frac{1}{3}3^{3}+c-\left(\frac{1}{3}1^{3}+c\right)\\ & =\frac{26}{3}. \end{align*}\]
Sometimes it is not possible to find the antiderivative. In such cases you need to use a numerical method. Two common methods for calculating definite integrals are:
Simpson’s rule, and
The trapezoidal rule.
This module considers the trapezoidal rule.
The Trapezoidal Rule
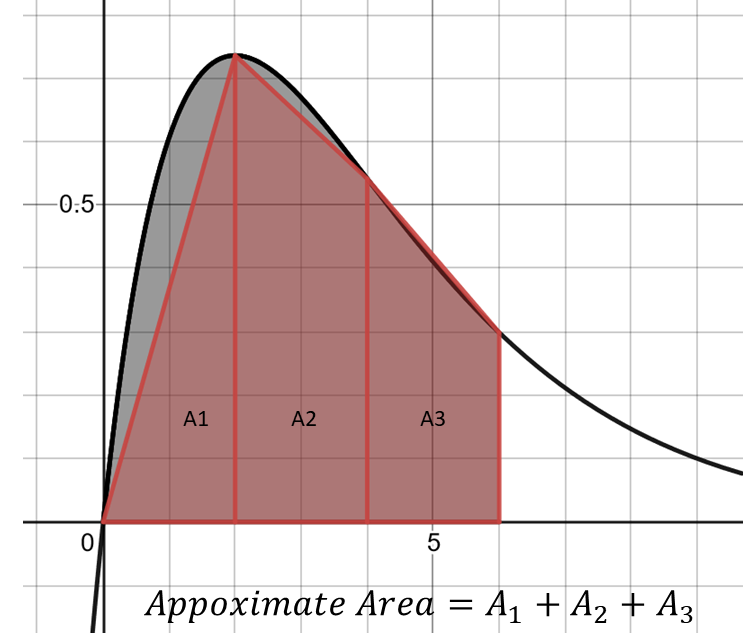
The trapezoidal rule works by estimating the area under a graph by a series of trapezoidal strips. In the figure below, we see an approximation to \[\begin{align*} \int_{1}^{6} & xe^{-0.5x}dx \end{align*}\] using three strips. The approximated area is shown in red.
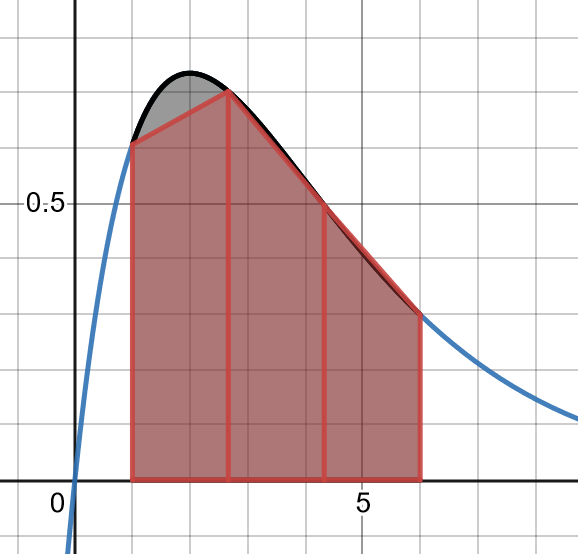
In this case, we see the trapezoidal rule will underestimate the first strip, is close in the second strip and will overestimate in the third strip. The trapezoidal rule approximates the area under the curve by adding the areas of the trapezoids. Any number of strips may be used. The accuracy increases as the number of strips increases.
For the definite integral \[\begin{align*} \int_{a}^{b}f\left(x\right)dx \end{align*}\] the trapezoidal rule has the form \[\begin{align*} \int_{a}^{b}f\left(x\right)dx & \approx\frac{h}{2}\left[y_{0}+2y_{1}+2y_{2}+\ldots+2y_{n-1}+y_{n}\right] & (1) \end{align*}\]
where
\(n\) is the number of strips and can be any number.
\(y_{n}=f\left(x_{n}\right)\) are the values of \(f\left(x_{n}\right)\) at the points \(x_{i}\) where \(i=0,1,2,\ldots,n\). Note that \(x_{0}=a,\) \(x_{n}=b.\)
\(h\) is the width of each strip and \[\begin{align*} h & =\frac{b-a}{n}. \end{align*}\]
\(x_{1}=a+h,\) \(x_{2}=a+2h,\) \(x_{3}=a+3h,\) \(\ldots\) and so on.
Example 1
Approximate \(\int_{0}^{6}xe^{-0.5x}dx\) using the trapezoidal rule with \(3\) strips , to \(3\) decimal places.
We have \(n=3\), \(a=x_{0}=0\) and \(b=x_{3}=6\) so \[\begin{align*} h & =\frac{b-a}{n}\\ & =\frac{6}{3}\\ & =2. \end{align*}\]
\(x_{0}=0\) and \(y_{0}=f\left(x_{0}\right)=0.\)
\(x_{1}=0+h=2\) and \(y_{1}=f\left(x_{1}\right)=2e^{-1}=0.73576.\)
\(x_{2}=0+2h=4\) and \(y_{2}=f\left(x_{2}\right)=4e^{-2}=0.54134.\)
\(x_{3}=0+3h=6\) and \(y_{3}=f\left(x_{3}\right)=6e^{-3}=0.29872.\)
Substituting into \(\left(1\right)\) above we get:
\[\begin{align*} \int_{0}^{6}xe^{-0.5x}dx & \approx\frac{2}{2}\left[y_{0}+2y_{1}+2y_{2}+y_{3}\right]\\ & =0+2\left(0.73576\right)+2\left(0.54134\right)+0.29872\\ & =2.85292. \end{align*}\] Hence, to three decimal places, \(\int_{0}^{6}xe^{-0.5x}dx\approx2.853.\)
Example 2
Approximate \(\int_{0}^{1}\sqrt{1+x^{3}}dx\) using the trapezoidal rule with \(5\) strips , to 3 decimal places.
In this question, \(n=5\), \(a=0\) and \(b=1\) so \[\begin{align*} h & =\frac{b-a}{n}\\ & =\frac{1}{5}\\ & =0.2\,. \end{align*}\] So using the formula above we get
\(x_{0}=0\) and \(y_{0}=f\left(x_{0}\right)=1.\)
\(x_{1}=0+h=0.2\) and \(y_{1}=f\left(x_{1}\right)=\sqrt{1+\left(0.2\right)^{3}}=1.00399.\)
\(x_{2}=0+2h=0.4\) and \(y_{2}=f\left(x_{2}\right)=\sqrt{1+\left(0.4\right)^{3}}=1.03150.\)
\(x_{3}=0+3h=0.6\) and \(y_{3}=f\left(x_{3}\right)=\sqrt{1+\left(0.6\right)^{3}}=1.10272.\)
\(x_{4}=0+4h=0.8\) and \(y_{4}=f\left(x_{4}\right)=\sqrt{1+\left(0.8\right)^{3}}=1.22963.\)
\(x_{5}=0+5h=1.0\) and \(y_{5}=f\left(x_{5}\right)=\sqrt{1+\left(1\right)^{3}}=1.41421.\)
Substituting into Substituting into \(\left(1\right)\) above we get:
\[\begin{align*} \int_{0}^{1}\sqrt{1+x^{3}}dx & \approx\frac{0.2}{2}\left[y_{0}+2y_{1}+2y_{2}+2y_{3}+2y_{4}+y_{5}\right]\\ & =0.1\left[1+2\left(1.00399\right)+2\left(1.03150\right)\right.\\ & \quad\quad\left.+2\left(1.10272\right)+2\left(1.22963\right)+1.41421\right]\\ & =1.11499. \end{align*}\] Hence, to three decimal places, \(\int_{0}^{1}\sqrt{1+x^{3}}dx\approx1.115.\)
Exercises
Use the trapezoidal rule to evaluate the integral \(\int_{1}^{3}\left(3x^{2}+4x\right)dx\) using 3 strips to two decimal places.
Use the trapezoidal rule to evaluate the integral \(\int_{0}^{1}\left(3e^{x}\sin\left(x\right)\right)dx\) using 2 strips to two decimal places.
Answers
42.44
2.90
Download this page, NM3 The trapezoidal rule (PDF 193KB)
What's next... NM4 Bisection method
