M9 Inverse of a 3x3 matrix
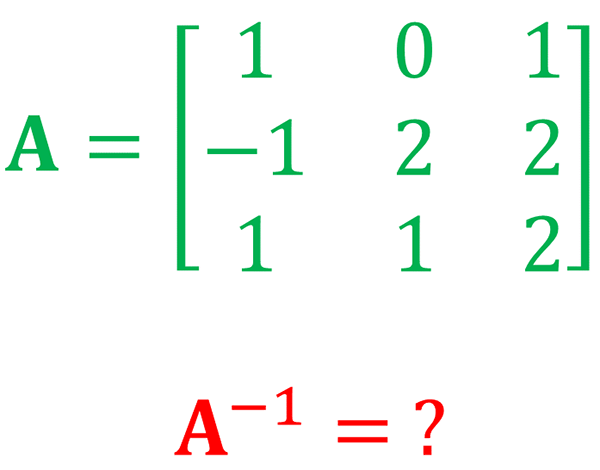
The \(3\times3\) identity matrix \[\begin{align*} \mathbf{I} & =\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]. \end{align*}\] If \(\mathbf{A}\) is a square matrix and \(\mathbf{B}\) is another square matrix of the same size, that is the same number of rows and columns, such that \[\begin{align*} {\bf AB} & ={\bf BA}={\bf I} \end{align*}\] then we call \({\bf B}\) the inverse of \(\mathbf{A}\). The inverse of \(\mathbf{A}\) is written as \(\mathbf{A}^{-1}.\) Therefore \[\begin{align*} \mathbf{A}\mathbf{A}^{-1} & ={\bf A}^{-1}{\bf A}={\bf I}. \end{align*}\]
Not every square matrix has an inverse. If a matrix does not have an inverse, it is called singular.
This module describes how to find the inverse of a \(3\times3\) matrix using elementary row operations.
Finding the Inverse
In theory, we use the matrix equation \[\begin{align*} {\bf AB} & ={\bf I} \end{align*}\] and pre-multiply both sides by \({\bf A}^{-1}\) (assuming it exists) to get \[\begin{align*} {\bf A}^{-1}{\bf AB} & ={\bf A}^{-1}{\bf {\bf I}}\\ {\bf I}{\bf B} & ={\bf A}^{-1}\\ {\bf B} & ={\bf A}^{-1}. \end{align*}\] In practice, we form the augmented matrix \[\begin{align*} \left[{\bf A}|{\bf I}\right] \end{align*}\] and use elementary row operations to convert this to \[\begin{align*} \left[{\bf I}|{\bf B}\right]. \end{align*}\] That is, for a \(3\times3\) matrix we use elementary row operations to change \[\begin{align*} \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right] \end{align*}\] to \[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\left|\begin{array}{c} \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\end{array}\right.\right] \end{align*}\] the matrix \[\begin{align*} {\bf B} & =\left[\begin{array}{c} \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\end{array}\right] \end{align*}\] is then the inverse \({\bf A}^{-1}.\)
Note that there are other methods to determine the inverse but they are not considered here.
Elementary Row Operations
Elementary row operations are:
Multiplication of a row by a constant;
Addition and subtraction of a multiple of a row to another row;
Interchanging two rows.
When using elementary row operations to find the inverse, there is a preferred order as shown in Figure 1 below.
\[\begin{align*} \underbrace{\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]}_{\text{1. Original matrix.}} & \rightarrow\underbrace{\left[\begin{array}{ccc} 1 & a_{12} & a_{13}\\ 0 & a_{22} & a_{23}\\ 0 & a_{32} & a_{33} \end{array}\right]}_{2.a_{11}=1,\,a_{21}=a_{23}=0}\rightarrow\underbrace{\left[\begin{array}{ccc} 1 & a_{12} & a_{13}\\ 0 & 1 & a_{23}\\ 0 & a_{32} & a_{33} \end{array}\right]}_{3.a_{22}=1}\rightarrow\underbrace{\left[\begin{array}{ccc} 1 & 0 & a_{13}\\ 0 & 1 & a_{23}\\ 0 & 0 & a_{33} \end{array}\right]}_{4.a_{12}=a_{32}=0}\rightarrow\underbrace{\left[\begin{array}{ccc} 1 & 0 & a_{13}\\ 0 & 1 & a_{23}\\ 0 & 0 & 1 \end{array}\right]}_{5.a_{31}=1}\rightarrow\underbrace{\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]}_{6.a_{13}=a_{23}=0}. \end{align*}\] Note that the \(a_{ij}\) may take new values at each step of the process.
If this looks confusing, don’t worry. It is easier to see with specific numbers as in the following examples.
Example \(1\)
Find the inverse of the matrix \({\bf A}=\left[\begin{array}{ccc} 1 & 0 & 1\\ -1 & 2 & 2\\ 1 & 1 & 2 \end{array}\right]\).
Solution:
Set up the augmented matrix \[\begin{align*} \left[{\bf A}|{\bf I}\right] & =\left[\begin{array}{ccc} 1 & 0 & 1\\ -1 & 2 & 2\\ 1 & 1 & 2 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right]. \end{align*}\] We now use row operations to reduce the matrix on the left hand side (LHS) to the identity matrix .
Returning to our problem, we already have a \(1\) in the \(a_{11}\) position of the LHS matrix so we first make \(a_{21}=a_{31}=0\) as follows
\[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 1\\ -1 & 2 & 2\\ 1 & 1 & 2 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right] & \begin{array}{c} \\ R_{2}+R_{1}\rightarrow R_{2}\\ R_{3}-R_{1}\rightarrow R_{3} \end{array}\left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 2 & 3\\ 0 & 1 & 1 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 1 & 1 & 0\\ -1 & 0 & 1 \end{array}\right.\right]. \end{align*}\] This completes Step \(2\) of figure \(1\) above.
Now we want \(a_{22}=1\) in the LHS matrix. There are two ways to do this. We could divide \(R_{2}\) by \(2\) however this introduces a fraction that may be awkward (fractions are commonly required but we delay their use until necessary). The other way, which we will use, is to interchange \(R_{2}\) and \(R_{3}\) as shown below:
\[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 2 & 3\\ 0 & 1 & 1 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 1 & 1 & 0\\ -1 & 0 & 1 \end{array}\right.\right] & \begin{array}{c} \\ R_{2}\rightarrow R_{3}\\ R_{3}\rightarrow R_{2} \end{array}\left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 2 & 3 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -1 & 0 & 1\\ 1 & 1 & 0 \end{array}\right.\right] \end{align*}\] This completes Step \(3\) figure \(1\) above and partially completes Step 4. Next we make \(a_{32}=0\) in the LHS matrix by subtracting \(2R_{2}\) from \(R_{3}.\) As a bonus this gives \(a_{33}=1\) in the LHS matrix:
\[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 2 & 3 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -1 & 0 & 1\\ 1 & 1 & 0 \end{array}\right.\right] & \begin{array}{c} \\ \\ R_{3}-2R_{2}\rightarrow R_{3} \end{array}\left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -1 & 0 & 1\\ 3 & 1 & -2 \end{array}\right.\right]. \end{align*}\] This completes Steps \(4\) and \(5\) of figure \(1\) above. Finally we make \(a_{13}=a_{23}=0\) using \(R_{3}\) as follows:
\[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -1 & 0 & 1\\ 3 & 1 & -2 \end{array}\right.\right] & \begin{array}{c} R_{1}-R_{3}\rightarrow R_{1}\\ R_{2}-R_{3}\rightarrow R_{2}\\ \\ \end{array}\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\left|\begin{array}{ccc} -2 & -1 & 2\\ -4 & -1 & 3\\ 3 & 1 & -2 \end{array}\right.\right]. \end{align*}\] This completes Step \(6\) of figure \(1\) above. The LHS matrix is the identity matrix and so the RHS is the inverse. That is \[\begin{align*} {\bf A}^{-1}=\left[\begin{array}{ccc} -2 & -1 & 2\\ -4 & -1 & 3\\ 3 & 1 & -2 \end{array}\right]. \end{align*}\] You should always check that \({\bf A}{\bf A}^{-1}={\bf A}^{-1}{\bf A}={\bf I}.\)1 Since in general, for matrices \({\bf A}\)and \({\bf B},\) \[\begin{align*} {\bf A}{\bf B} & \neq{\bf B}{\bf A} \end{align*}\] it is important to check both \({\bf A}{\bf A}^{-1}={\bf I}\) and \({\bf A}^{-1}{\bf A}={\bf I}.\) We have \[\begin{align*} {\bf A}{\bf A}^{-1} & =\left[\begin{array}{ccc} 1 & 0 & 1\\ -1 & 2 & 2\\ 1 & 1 & 2 \end{array}\right]\left[\begin{array}{ccc} -2 & -1 & 2\\ -4 & -1 & 3\\ 3 & 1 & -2 \end{array}\right]\\ & =\left[\begin{array}{ccc} -2+3 & -1+1 & 2-2\\ 2-8+6 & 1-2+2 & -2+6-4\\ -2-4+6 & -1-1+2 & 2+3-4 \end{array}\right]\\ & =\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\\ & ={\bf I} \end{align*}\] and \[\begin{align*} {\bf A}^{-1}{\bf A} & =\left[\begin{array}{ccc} -2 & -1 & 2\\ -4 & -1 & 3\\ 3 & 1 & -2 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 1\\ -1 & 2 & 2\\ 1 & 1 & 2 \end{array}\right]\\ & =\left[\begin{array}{ccc} -2+1+2 & -2+2 & -2-2+4\\ -4+1+3 & -2+3 & -4-2+6\\ 3-1-2 & 2-2 & 3+2-4 \end{array}\right]\\ & =\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\\ & ={\bf I} \end{align*}\] Hence \[\begin{align*} {\bf A}^{-1}=\left[\begin{array}{ccc} -2 & -1 & 2\\ -4 & -1 & 3\\ 3 & 1 & -2 \end{array}\right]. \end{align*}\]
Example \(2\)
Find the inverse of \({\bf B}=\left[\begin{array}{ccc} 1 & -1 & -1\\ 3 & -2 & 1\\ -1 & 1 & 3 \end{array}\right].\)
Solution:
The augmented matrix is: \[\begin{align*} \left[{\bf B}|{\bf I}\right] & =\left[\begin{array}{ccc} 1 & -1 & -1\\ 3 & -2 & 1\\ -1 & 1 & 3 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right]. \end{align*}\]
Starting row operations: \[\begin{align*} \left[\begin{array}{ccc} 1 & -1 & -1\\ 3 & -2 & 1\\ -1 & 1 & 3 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right]\begin{array}{c} \\ R_{2}-3R_{1}\rightarrow R_{2}\\ R_{3}+R_{1}\rightarrow R_{3} \end{array} & \left[\begin{array}{ccc} 1 & -1 & -1\\ 0 & 1 & 4\\ 0 & 0 & 2 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -3 & 1 & 0\\ 1 & 0 & 1 \end{array}\right.\right] \end{align*}\]
\[\begin{align*} \left[\begin{array}{ccc} 1 & -1 & -1\\ 0 & 1 & 4\\ 0 & 0 & 2 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -3 & 1 & 0\\ 1 & 0 & 1 \end{array}\right.\right]\begin{array}{c} R_{1}+R_{2}\rightarrow R_{1}\\ \\ \\ \end{array} & \left[\begin{array}{ccc} 1 & 0 & 3\\ 0 & 1 & 4\\ 0 & 0 & 2 \end{array}\left|\begin{array}{ccc} -2 & 1 & 0\\ -3 & 1 & 0\\ 1 & 0 & 1 \end{array}\right.\right] \end{align*}\]
\[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 3\\ 0 & 1 & 4\\ 0 & 0 & 2 \end{array}\left|\begin{array}{ccc} -2 & 1 & 0\\ -3 & 1 & 0\\ 1 & 0 & 1 \end{array}\right.\right]\begin{array}{c} \\ \\ R_{3}\div2\rightarrow R_{3} \end{array} & \left[\begin{array}{ccc} 1 & 0 & 3\\ 0 & 1 & 4\\ 0 & 0 & 1 \end{array}\left|\begin{array}{ccc} -2 & 1 & 0\\ -3 & 1 & 0\\ 1/2 & 0 & 1/2 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \left[\begin{array}{ccc} 1 & 0 & 3\\ 0 & 1 & 4\\ 0 & 0 & 1 \end{array}\left|\begin{array}{ccc} -2 & 1 & 0\\ -3 & 1 & 0\\ 1/2 & 0 & 1/2 \end{array}\right.\right]\begin{array}{c} R_{1}-3R_{3}\rightarrow R_{1}\\ R_{2}-4R_{3}\rightarrow R_{2}\\ \\ \end{array} & \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\left|\begin{array}{ccc} -7/2 & 1 & -3/2\\ -5 & 1 & -2\\ 1/2 & 0 & 1/2 \end{array}\right.\right]. \end{align*}\] Hence subject to checking \({\bf B}{\bf B}^{-1}={\bf B}^{-1}{\bf B}={\bf I},\) \[\begin{align*} {\bf B}^{-1} & =\left[\begin{array}{ccc} -7/2 & 1 & -3/2\\ -5 & 1 & -2\\ 1/2 & 0 & 1/2 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{ccc} -7 & 2 & -3\\ -10 & 2 & -4\\ 1 & 0 & 1 \end{array}\right]. \end{align*}\]
Check: \[\begin{align*} {\bf B}{\bf B}^{-1} & =\left[\begin{array}{ccc} 1 & -1 & -1\\ 3 & -2 & 1\\ -1 & 1 & 3 \end{array}\right]\frac{1}{2}\left[\begin{array}{ccc} -7 & 2 & -3\\ -10 & 2 & -4\\ 1 & 0 & 1 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{ccc} 1 & -1 & -1\\ 3 & -2 & 1\\ -1 & 1 & 3 \end{array}\right]\left[\begin{array}{ccc} -7 & 2 & -3\\ -10 & 2 & -4\\ 1 & 0 & 1 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{ccc} -7+10-1 & 2-2 & -3+4-1\\ -21+20+1 & 6-4 & -9+8+1\\ 7-10+3 & -2+2 & 3-4+3 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{ccc} 2 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 2 \end{array}\right]\\ & ={\bf I} \end{align*}\] and \[\begin{align*} {\bf B}^{-1}{\bf B} & =\frac{1}{2}\left[\begin{array}{ccc} -7 & 2 & -3\\ -10 & 2 & -4\\ 1 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & -1 & -1\\ 3 & -2 & 1\\ -1 & 1 & 3 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{ccc} -7+6+3 & 7-4-3 & 7+2-9\\ -10+6+4 & 10-4-4 & 10+2-12\\ 1-1 & -1+1 & -1+3 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{ccc} 2 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 2 \end{array}\right]\\ & ={\bf I}. \end{align*}\] Hence, \[\begin{align*} {\bf B}^{-1} & =\frac{1}{2}\left[\begin{array}{ccc} -7 & 2 & -3\\ -10 & 2 & -4\\ 1 & 0 & 1 \end{array}\right]. \end{align*}\]
Example \(3\) (No inverse exists)
Find the inverse of \({\bf C}=\left[\begin{array}{ccc} 1 & 2 & 2\\ 1 & 1 & 2\\ 1 & 0 & 2 \end{array}\right].\)
Solution:
The augmented matrix is: \[\begin{align*} \left[{\bf C}|{\bf I}\right] & =\left[\begin{array}{ccc} 1 & 2 & 2\\ 1 & 1 & 2\\ 1 & 3 & 2 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right]. \end{align*}\] Starting row operations: \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & 2\\ 1 & 1 & 2\\ 1 & 3 & 2 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right.\right]\begin{array}{c} \\ R_{2}-R_{1}\rightarrow R_{2}\\ R_{3}-R_{1}\rightarrow R_{3} \end{array} & \left[\begin{array}{ccc} 1 & 2 & 2\\ 0 & -1 & 0\\ 0 & 1 & 0 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -1 & 1 & 0\\ -1 & 0 & 1 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & 2\\ 0 & -1 & 0\\ 0 & 1 & 0 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ -1 & 1 & 0\\ -1 & 0 & 1 \end{array}\right.\right]\begin{array}{c} \\ \\ R_{3}+R_{2}\rightarrow R_{3} \end{array} & \left[\begin{array}{ccc} 1 & 2 & 3\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{array}\left|\begin{array}{ccc} 1 & 0 & 0\\ 1 & -1 & 0\\ 0 & -1 & 1 \end{array}\right.\right] \end{align*}\]
The LHS matrix in the augmented matrix has it’s third row consisting of zeros. It is impossible to transform this matrix into the identity using row operations. Hence this matrix is singular and no inverse exists.
Existence of an Inverse
A square matrix \({\bf A}\) has an inverse if and only if it’s determinant is unequal to zero. We don’t discuss this further in this module.
Exercises
Find the inverse, if it exists, of the following matrices.
\(\text{1. $\left[\begin{array}{ccc} 0 & 0 & -1\\ 2 & 1 & 2\\ 5 & 3 & 0 \end{array}\right]$ }\)
\(\text{2. $\left[\begin{array}{ccc} 1 & 2 & 0\\ -1 & 3 & 1\\ 2 & 5 & 2 \end{array}\right]$ }\)
\(\text{3. $\left[\begin{array}{ccc} 1 & 2 & 0\\ 1 & 2 & 1\\ 1 & 2 & 4 \end{array}\right]$ }\)
\(\text{4. $\left[\begin{array}{ccc} -2 & 2 & 0\\ 1 & 0 & 1\\ 1 & -1 & -2 \end{array}\right]$ }\)
\(\text{1. $\left[\begin{array}{ccc} 6 & 3 & -1\\ -10 & -5 & 2\\ -1 & 0 & 0 \end{array}\right]$ }.\)
\(\text{2. $\,\frac{1}{9}\left[\begin{array}{ccc} 1 & -4 & 2\\ 4 & 2 & -1\\ -11 & -1 & 5 \end{array}\right]$ }.\)
\(\text{3. No inverse exists}.\)
\(\text{4. $\,\frac{1}{4}\left[\begin{array}{ccc} 1 & 4 & 2\\ 3 & 4 & 2\\ -1 & 0 & -2 \end{array}\right].$ }\)
Download this page, M9 Inverse of a 3x3 Matrix (PDF 137KB)
What's next... M10 Eigenvalues and eigenvectors
