M2 Addition and subtraction of matrices
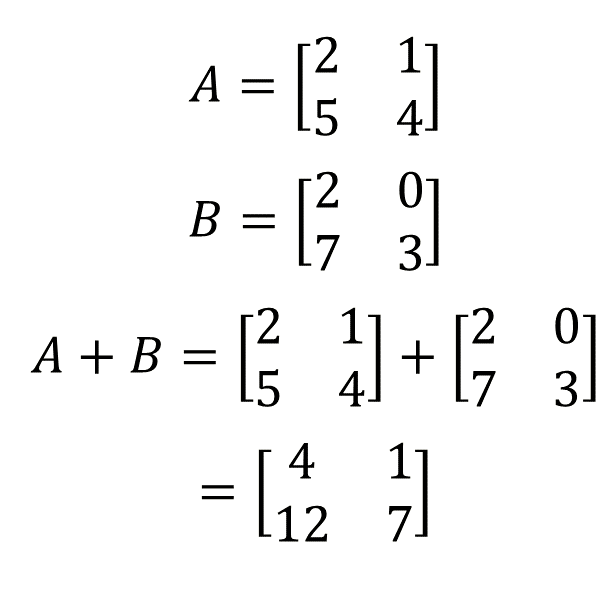
A matrix is an array of numbers. There are rules for adding and subtracting matrices and these are reviewed in this module. Matrices of the same shape (same number of rows and columns) may be added and subtracted.
Addition
Matrices of the same shape (same number of rows and columns) may be added by adding the corresponding elements.
For example, let \[\begin{align*} A & =\left[\begin{array}{ccc} 3 & 2 & -1\\ 1 & 5 & -4 \end{array}\right],\,B=\left[\begin{array}{ccc} 1 & 0 & 2\\ 3 & 1 & -2 \end{array}\right]\;\textrm{and $C=\left[\begin{array}{cc} 2 & -3\\ 4 & 3 \end{array}\right]$ }. \end{align*}\] Notice that \(A\) and \(B\) are the same shape \(\left(2\times3\right)\) and \(C\) is \(\left(2\times2\right)\).
Then \(A+B\) makes sense because they are both \(\left(2\times3\right)\) and we have \[\begin{align*} A+B & =\left[\begin{array}{ccc} 3 & 2 & -1\\ 1 & 5 & -4 \end{array}\right]+\left[\begin{array}{ccc} 1 & 0 & 2\\ 3 & 1 & -2 \end{array}\right]\\ & =\left[\begin{array}{ccc} 3+1 & 2+0 & -1+2\\ 1+3 & 5+1 & -4+(-2) \end{array}\right]\\ & =\left[\begin{array}{ccc} 4 & 2 & 1\\ 4 & 6 & -6 \end{array}\right]. \end{align*}\]
However \(A+C\) is not defined as \(A\) is \(\left(2\times3\right)\) and \(C\) is \(\left(2\times2\right)\). You cannot add matrices that have different shape.
Note that the order of addition is the same as for real numbers. That is: \[\begin{align*} A+B & =B+A \end{align*}\]
Subtraction
Matrices of the same the shape may be subtracted by subtracting corresponding elements. For example, let \[\begin{align*} A & =\left[\begin{array}{ccc} 3 & 2 & -1\\ 1 & 5 & -4 \end{array}\right],\,B=\left[\begin{array}{ccc} 1 & 0 & 2\\ 3 & 1 & -2 \end{array}\right]\;\textrm{and $C=\left[\begin{array}{cc} 2 & -3\\ 4 & 3 \end{array}\right]$ }. \end{align*}\] Then \(A-B\) makes sense because they are both \(\left(2\times3\right)\) and we have \[\begin{align*} A-B & =\left[\begin{array}{ccc} 3 & 2 & -1\\ 1 & 5 & -4 \end{array}\right]-\left[\begin{array}{ccc} 1 & 0 & 2\\ 3 & 1 & -2 \end{array}\right]\\ & =\left[\begin{array}{ccc} 3-1 & 2-0 & -1-2\\ 1-3 & 5-1 & -4-(-2) \end{array}\right]\\ & =\left[\begin{array}{ccc} 2 & 2 & -3\\ -2 & 4 & -2 \end{array}\right]. \end{align*}\]
However \(A-C\) is not defined as \(A\) is \(\left(2\times3\right)\) and \(C\) is \(\left(2\times2\right)\). You cannot subtract matrices that have different shape. As another example consider \(B-A\) we have \[\begin{alignat*}{1} B-A & =\left[\begin{array}{ccc} 1 & 0 & 2\\ 3 & 1 & -2 \end{array}\right]-\left[\begin{array}{ccc} 3 & 2 & -1\\ 1 & 5 & -4 \end{array}\right]\\ & =\left[\begin{array}{ccc} 1-3 & 0-2 & 2-(-1)\\ 3-1 & 1-5 & -2-(-4) \end{array}\right]\\ & =\left[\begin{array}{ccc} -2 & -2 & 3\\ 2 & -4 & 2 \end{array}\right] \end{alignat*}\] Note that \(A-B\neq B-A\). The order in which matrices are subtracted is important just as it is when subtracting real numbers. In fact, \(B-A=-\left(A-B\right)\).
Scalar Multiplication
Matrices may be multiplied by a number. To do this each element in the matrix is multiplied by the number.
For example, let \[\begin{align*} A & =\left[\begin{array}{cc} 1 & 2\\ 5 & 4 \end{array}\right]\textrm{ and $B=\left[\begin{array}{cc} 2 & -3\\ 0 & -1 \end{array}\right]$ } \end{align*}\] then \[\begin{align*} 5A & =5\times\left[\begin{array}{cc} 1 & 2\\ 5 & 4 \end{array}\right]\\ & =\left[\begin{array}{cc} 5\times1 & 5\times2\\ 5\times5 & 5\times4 \end{array}\right]\\ & =\left[\begin{array}{cc} 5 & 10\\ 25 & 20 \end{array}\right]. \end{align*}\]
Another example is \[\begin{align*} -2A & =-2\times\left[\begin{array}{cc} 1 & 2\\ 5 & 4 \end{array}\right]\\ & =\left[\begin{array}{cc} -2\times1 & -2\times2\\ -2\times5 & -2\times4 \end{array}\right]\\ & =\left[\begin{array}{cc} -2 & -4\\ -10 & -8 \end{array}\right]. \end{align*}\]
You can also use scalar multiplication with addition or subtraction. For example: \[\begin{align*} 5A-2B & =5\times\left[\begin{array}{cc} 1 & 2\\ 5 & 4 \end{array}\right]-2\times\left[\begin{array}{cc} 2 & -3\\ 0 & -1 \end{array}\right]\\ & =\left[\begin{array}{cc} 5\times1 & 5\times2\\ 5\times5 & 5\times4 \end{array}\right]-\left[\begin{array}{cc} 2\times2 & 2\times\left(-3\right)\\ 2\times0 & 2\times\left(-1\right) \end{array}\right]\\ & =\left[\begin{array}{cc} 5 & 10\\ 25 & 20 \end{array}\right]-\left[\begin{array}{cc} 4 & -6\\ 0 & -2 \end{array}\right]\\ & =\left[\begin{array}{cc} 5-4 & 10-\left(-6\right)\\ 25-0 & 20-\left(-2\right) \end{array}\right]\\ & =\left[\begin{array}{cc} 1 & 16\\ 25 & 22 \end{array}\right]. \end{align*}\]
Exercises
Given \[\begin{align*} A & =\left[\begin{array}{c} 2\\ 3 \end{array}\right],\;B=\left[\begin{array}{cc} 1 & 2\\ 4 & 3 \end{array}\right],\;C=\left[\begin{array}{cc} 5 & 3\\ -1 & 2 \end{array}\right],\;D=\left[\begin{array}{cc} 2 & 3\end{array}\right],\;E=\left[\begin{array}{cc} -1 & 0\\ 2 & -1 \end{array}\right], \end{align*}\] find if possible: \[\begin{align*} \begin{array}{lllll} a)\,A+B & b)\,B-C & c)\,A-D & d)\,B+E & e)\,E-D.\end{array} \end{align*}\]
Given \[\begin{align*} A=\left[\begin{array}{ccc} 2 & 3 & 1\\ 0 & 1 & 2 \end{array}\right],\;B=\left[\begin{array}{c} 4\\ -1\\ 2 \end{array}\right],\;C=\left[\begin{array}{ccc} 1 & -1 & 2\\ 2 & 0 & 1 \end{array}\right],\;D=\left[\begin{array}{c} 1\\ 0\\ -1 \end{array}\right],\;E=\left[\begin{array}{ccc} 0 & 1 & 3\\ 1 & 0 & 2 \end{array}\right], \end{align*}\] find if possible: \[\begin{align*} \begin{array}{lllll} a)\,2A+B & b)\,4D-B & c)\,3C-A & d)\,B+2D+E & e)\,3C-A+2E\end{array}. \end{align*}\]
\[\begin{align*} \begin{array}{llllll} 1. & a)\,\textrm{Not possible} & b)\,\left[\begin{array}{cc} -4 & -1\\ 5 & 1 \end{array}\right] & c)\,\textrm{Not possible} & d)\,\left[\begin{array}{cc} 0 & 2\\ 6 & 2 \end{array}\right] & e)\,\textrm{Not possible}.\end{array} \end{align*}\]
\[\begin{align*} \begin{array}{llllll} 2. & a)\,\textrm{Not possible} & b)\,\left[\begin{array}{c} 0\\ -1\\ -6 \end{array}\right] & c)\,\left[\begin{array}{ccc} 1 & -6 & 5\\ 6 & -1 & 1 \end{array}\right] & d)\,\textrm{Not possible} & e)\,\left[\begin{array}{ccc} 1 & -4 & 11\\ 8 & -1 & 5 \end{array}\right].\end{array} \end{align*}\]
Download this page, M2 Addition and subtraction of matrices (PDF 110KB)
What's next... M3 Matrix multiplication
