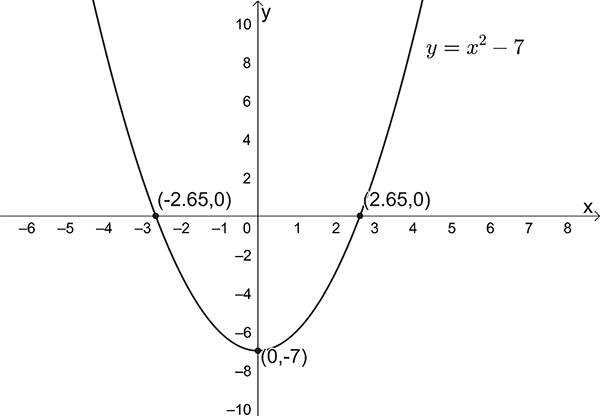FG8 Quadratic graphs
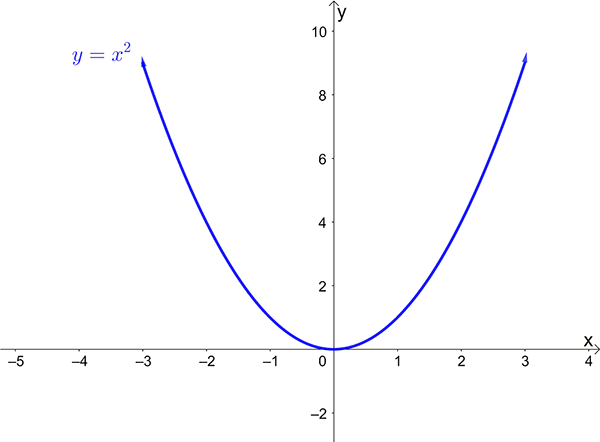
The graph of a quadratic function is called a parabola.
A quadratic graph is the graph of a quadratic function. This module describes the graphing of quadratic functions. A quadratic function has the form \(y=ax^{2}+bx+c\) where \(a\neq0\) .
The graph of a quadratic function is called a parabola.
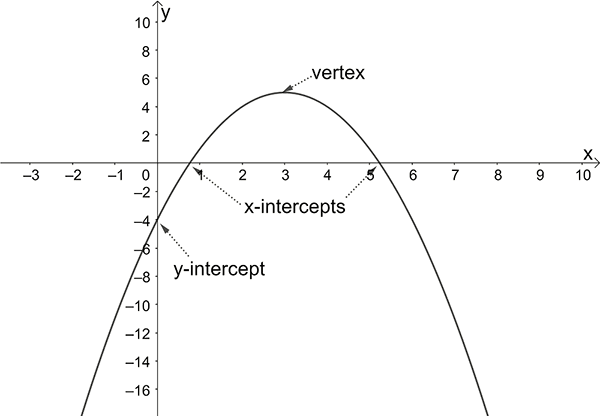
To sketch a parabola, find and label:
the \(y\)-intercept (put \(x=0\))
the \(x\)-intercepts (put \(y=0\))
the vertex (turning point)
The co-ordinates of the vertex are given by:
\(x\) co-ordinate \(\left(-\dfrac{b}{2a}\right)\)
\(y\) co-ordinate: substitute the value of the \(x\) co-ordinate in the equation for \(y\).
A parabola is symmetrical about a vertical line through the vertex.
If \(a>0\), then the parabola opens upwards (and has a minimum turning point).
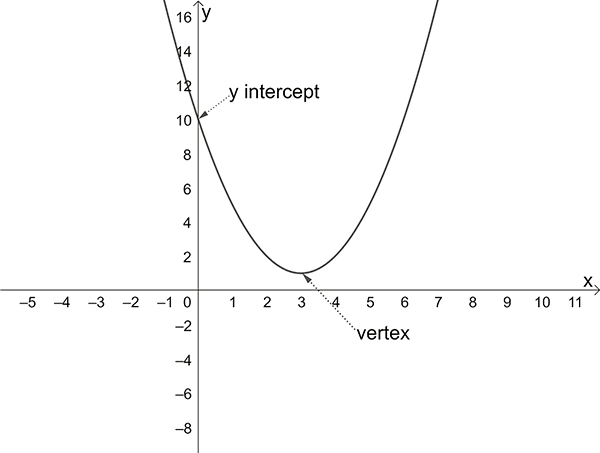
If \(a<0\), then the parabola opens downwards (and has a maximum turning point).
A quadratic function may also be written in turning point form: \(y=a(x-h)^{2}+k\) , where \((h,k)\) is the turning point.
Examples
\(y=(x-3)^{2}+4\) has a turning point at \((3,4)\)
\(y=(x+5)^{2}+2\) has a turning point at \((-5,2)\)
\(y=2(x+1)^{2}\) can be written as \(y=2(x+1)^{2}+0\) and has a turning point at \((-1,0)\)
\(y=x^{2}-7\) can be written as \(y=(x-0)^{2}-7\) and has a turning point at \((0,-7)\)
\(y=6-(x-2)^{2}\) can be written as \(y=-(x-2)^{2}+6\) and has a turning point at \((2,6)\)
See Exercise 1
Sketching a Parabola
To sketch a parabola, find and label:
the \(y\)-intercept (put \(x=0\))
the \(x\)-intercepts (put \(y=0\))
the vertex (turning point)
Examples
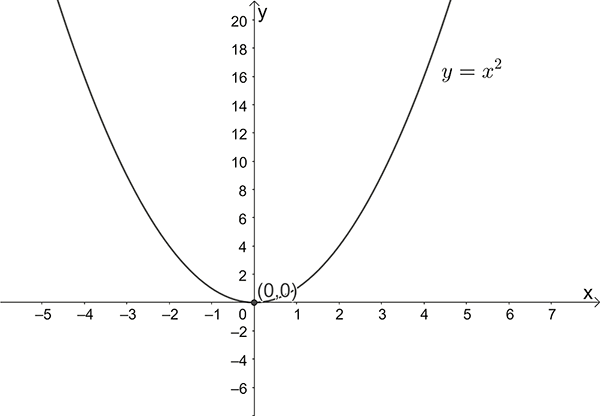
- Sketch \(y=x^{2}\)
Intercepts \(x=0\) , \(y=0\)
Turning point \((0,0)\)
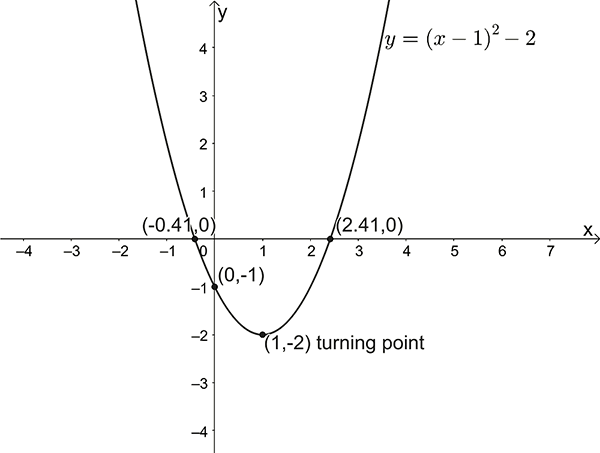
- Sketch \(y=(x-1)^{2}-2\)
\(y\)-intercept: \(x=0\) , \(y=-1\)
\(x\)-intercepts: \(y=0\) , \(x=\pm\sqrt{2}+1\)
Turning point: \((1,-2)\)
- Sketch \(y=x^{2}+3\)
\(y\)-intercept: \(x=0\) , \(y=3\)
\(x\)-intercepts: \(y=0\) , \(0=x^{2}+3\Rightarrow x^{2}=-3\) no solution, no \(x\)-intercepts
Turning point: \((0,3)\)
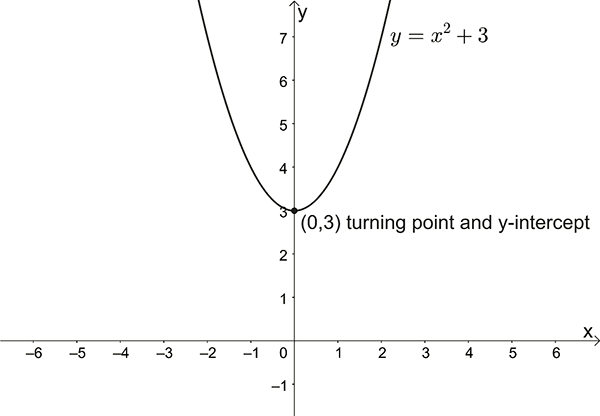
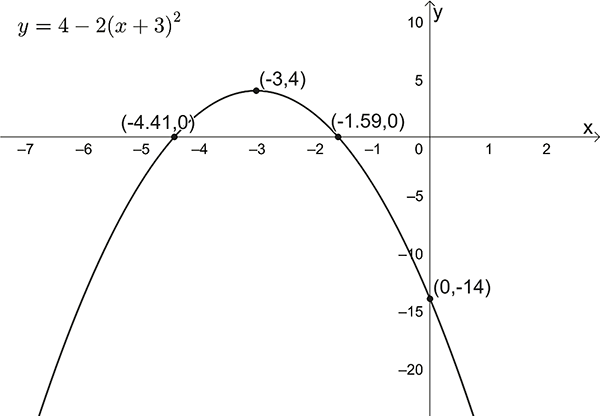
- Sketch \(y=4-2(x+3)^{2}\)
\(y\)-intercept: \(x=0\) , \(y=-14\)
\(x\)-intercepts: \(y=0\) ,
\(0=4-2(x+3)^{2}\)
\(\Rightarrow(x+3)^{2}=2\)
\(\Rightarrow x+3=\pm\sqrt{2}\)
\(\Rightarrow x=-3\pm\sqrt{2}\)
Turning point: \((-3,4)\)
See Exercise 2
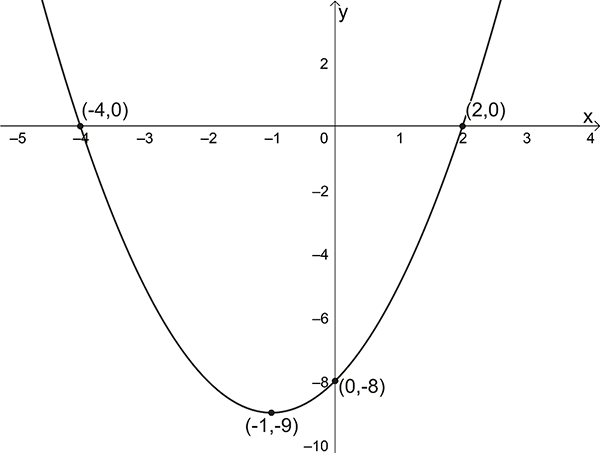
- Sketch the graph \(y=x^{2}+2x-8\)
\(y\)-intercept: \(x=0\) , \(y=-8\)
\(x\)-intercepts: \(y=0\) ,
\(0=x^{2}+2x-8\)
\(\Rightarrow0=(x+4)(x-2)\)
\(\Rightarrow x=-4\) or \(x=2\)
Turning point: This equation is not in turning point form so we use the equation for the \(x\)-coordinate of the turning point: \(x=\left(-\dfrac{b}{2a}\right)\)
In this example \(a=1\) , \(b=2\)
therefore, the \(x\)-coordinate of the turning point is \(\left(-\dfrac{2}{2\times1}\right)=-1\)
Since \(y=x^{2}+2x-8\) the \(y\)-coordinate of the turning point is \(y=(-1)^{2}+2(-1)-8=-9\)
\(T.P.=(-1,-9)\)
See Exercise 3
Exercise 1
State the turning point of the graphs of the following functions.
\(y=(x-1)^{2}+5\)
\(y=5(x-4)^{2}-12\)
\(y=(x+2)^{2}+3\)
\(y=-3(x+5)^{2}-3\)
\(y=(x-6)^{2}\)
\(y=-4x^{2}+3\)
- \((1,5)\ \ \ \) (b) \((4,12)\ \ \ \) (c) \((2,3)\ \ \ \) (d) \((5,3)\ \ \ \) (e) \((6,0)\ \ \ \) (f) \((0,3)\)
Exercise 2
Sketch graphs of the following.
\(y=x^{2}-7\)
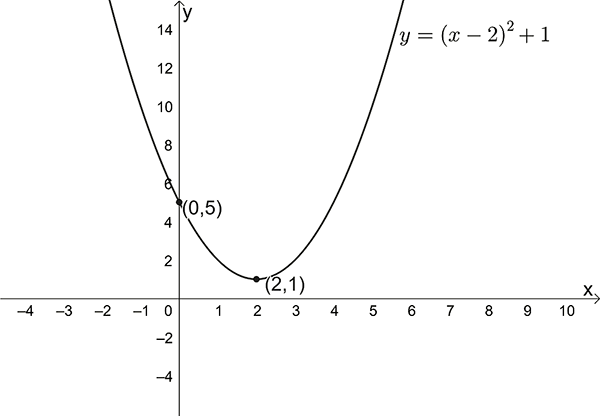
\(y=(x-2)^{2}+1\)
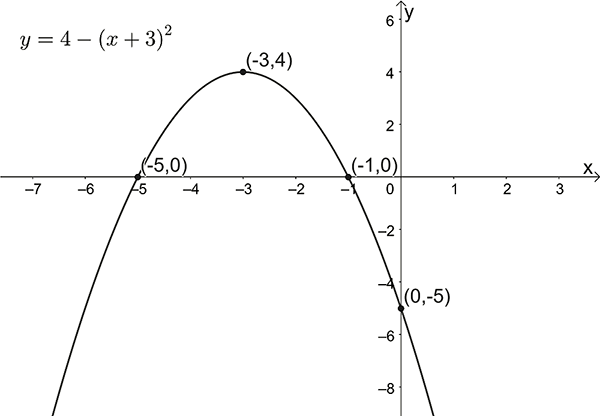
\(y=4-(x+3)^{2}\)
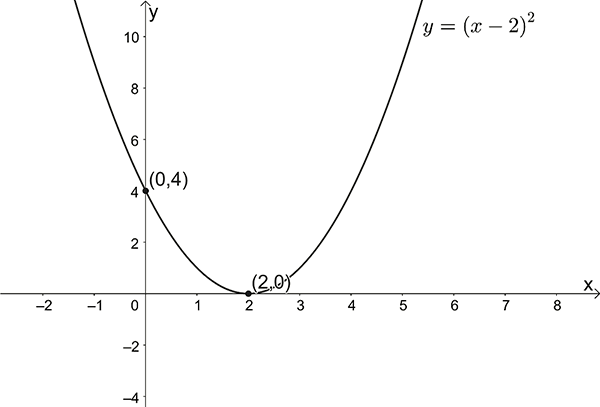
\(y=(x-2)^{2}\)
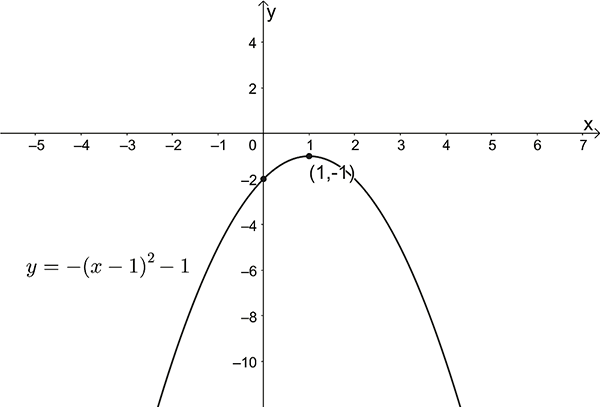
\(y=-(x-1)^{2}-1\)
Exercise 3
Sketch the graphs of the following functions:
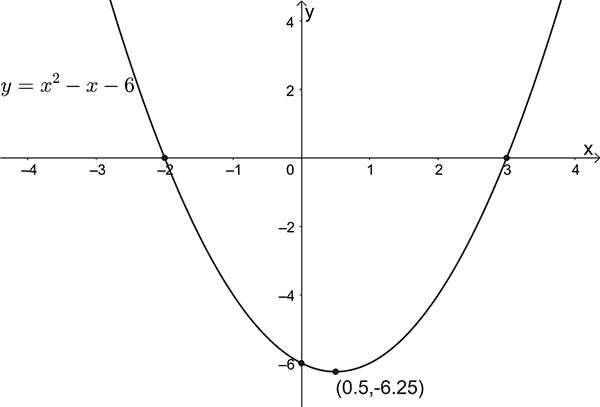
\(y=x^{2}-x-6\)
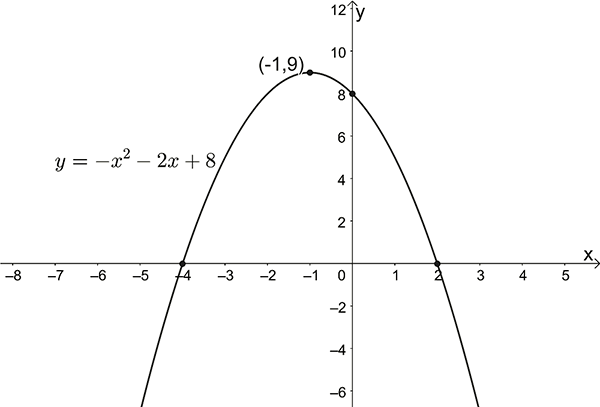
\(y=-x^{2}-2x+8\)
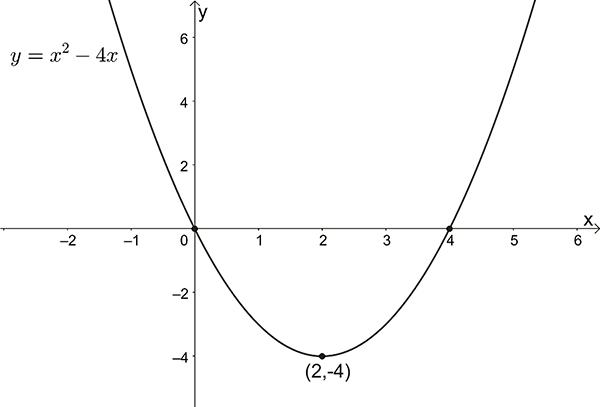
\(y=x^{2}-4x\)
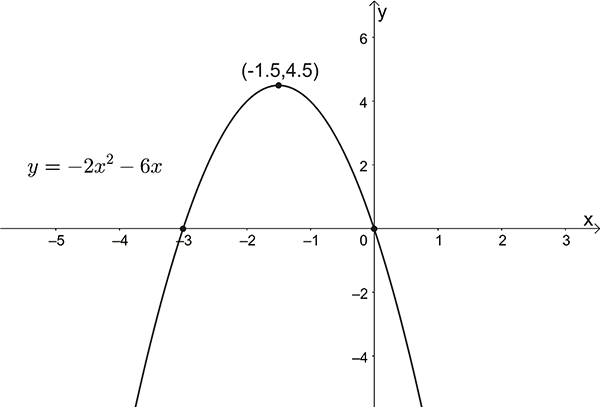
\(y=-2x^{2}-6x\)
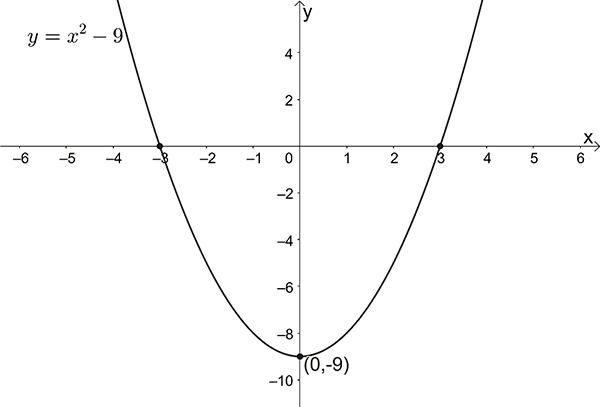
\(y=x^{2}-9\)
Download this page, FG8 Quadratic Graphs (PDF 821KB)
What's next... FG9 Graphs and transformations