FG7 Linear graphs
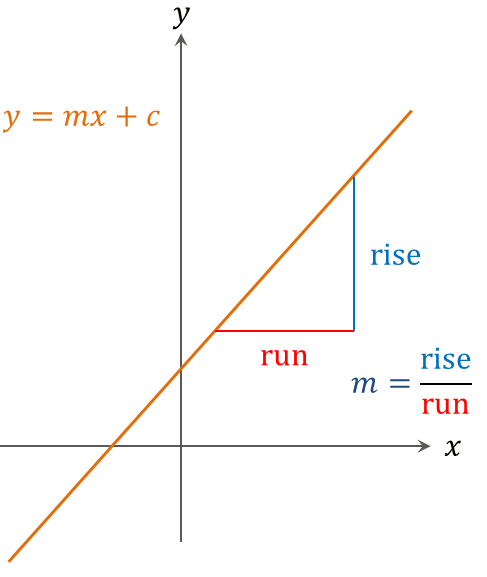
A linear graph is the simplest way of representing data or a functional relationship. Consequently an understanding of linear graphs is an essential requirement for many courses in science, engineering and mathematics. This module deals with linear graphs.
The Cartesian Plane
The Cartesian plane is defined by a pair of mutually perpendicular coordinate axes. The horizontal axis is the x- axis and the vertical axis the y – axis. Their point of intersection is called the origin O.
Points on the plane are referred to by their horizontal distance (\(x\) – coordinate) and vertical distance (\(y\) – coordinate) from the origin. Distances to the right of, and up from the origin are positive. Distances to the left of, and down from the origin are negative. Consider the figure below.
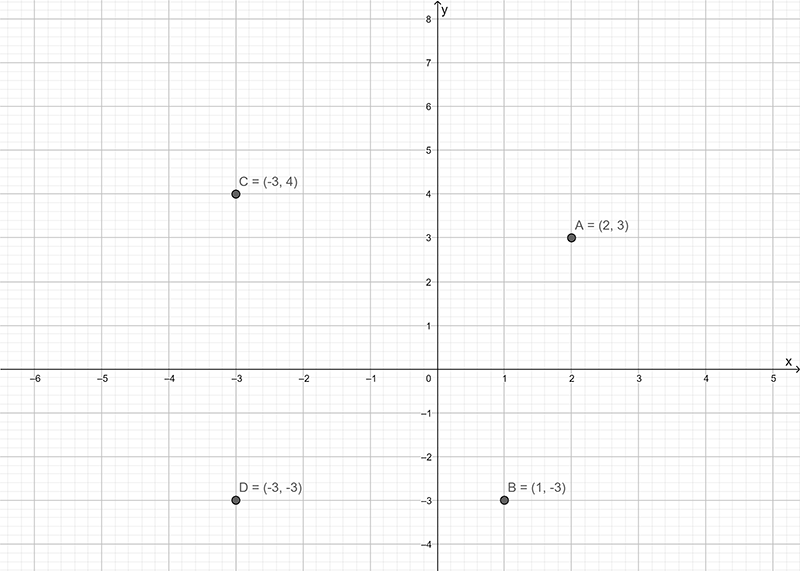
The \(x\) – coordinate is always given first.
The point A (\(2,3\)) has coordinates \(x=2\) and \(y=3\).
The point B (\(1,3\)) has coordinates \(x=1\) and \(y=3\).
The point C (\(3,3\)) has coordinates \(x=3\) and \(y=3\).
The point D (\(3,4\)) has coordinates \(x=3\) and \(y=4\).
Sketch Graphs
When sketching a graph it is not necessary to plot large numbers of points. Only the basic shape of the graph is required, although some important points need to be clearly labeled.
Intercepts
These are the points where the graph crosses the \(x\) and \(y\) axes. The \(x\)-intercept is where the graph cuts the \(x\)-axis \(\left(y=0\right)\) and the \(y\)-intercept is where the graph cuts the \(y\)-axis \(\left(x=0\right)\).
Linear Graphs
The graph of a linear relationship is a straight line. Only two points are needed to sketch the graph of a straight line.
Example
Sketch the function \(y=3x+6\).
Solution:
Determine two points on the line.
The \(x\) and \(y\)-intercepts are often the easiest to find.
For the \(y\)- intercept \(\left(x=0\right)\), we have \[\begin{align*}
y & =3x+6\\
& =6.
\end{align*}\] Hence the \(y\)-intercept is at \(\left(0,6\right)\).
Now we want the \(x\)- intercept \(\left(y=0\right).\) So \[\begin{align*}
y & =3x+6\\
0 & =3x+6\\
3x & =-6\\
x & =-2.
\end{align*}\]
Hence the \(x\)-intercept is at \(\left(-2,0\right).\)
The y-intercept is the point \((0,6\)).
\[\begin{align*} x\textrm{-intercept} & (y=0)\\ \textrm{When }y & =0\\ 0 & =3x+6\\ 3x & =-6\\ x & =-2 \end{align*}\]
The x-intercept is the point ( 2, 0).
Connect the two points with a straight line.
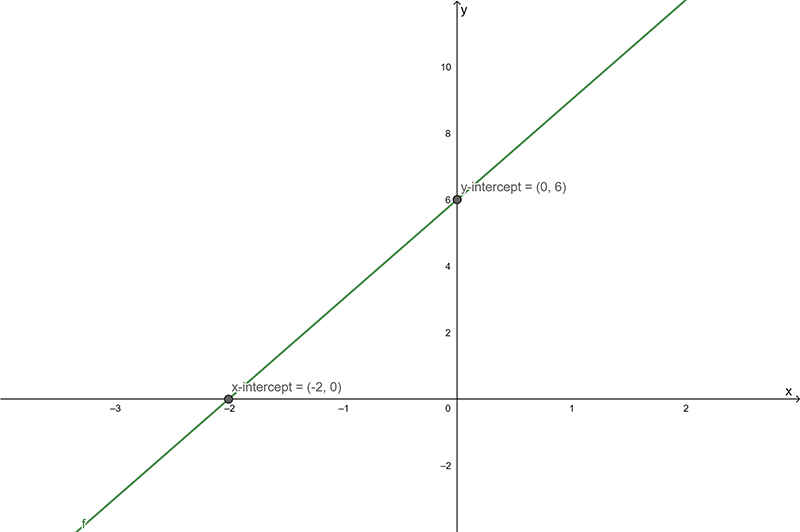
The \(x\)- and \(y\)-intercepts should be marked on the graph.
See Exercise 1
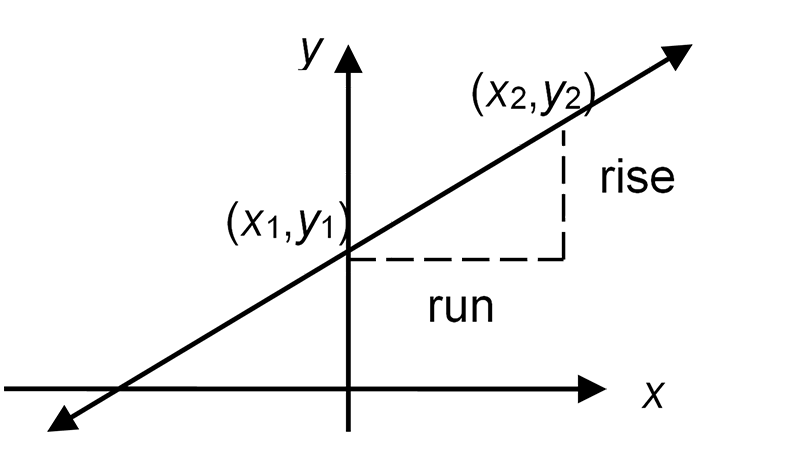
Gradient
The slope of the straight line is called the gradient. This is the ratio of the vertical change (rise) to the horizontal change (run) between two points (\(x_{1},y_{1}\)) and (\(x_{2},y_{2}\)) on the line.
\[\begin{align*} Gradient & =\frac{rise}{run}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \end{align*}\]
Examples
Find the gradient of the line \(y=3x+6\) (see previous example).
Solution:
The points (\(0,6\)) and (\(-2,0\)) are on the line \(y=3x+6\).1 Note that it doesn’t matter which points you choose for \(\left(x_{1},y_{1}\right)\) and \(\left(x_{2},y_{2}\right)\). The only requirement is that both points must be on the line. For example we could let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(-2,0\right) \end{align*}\] \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(0,6\right) \end{align*}\] then \[\begin{align*} Gradient & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\ & =\frac{6-0}{0-\left(-2\right)}\\ & =3 \end{align*}\] the same answer as at left. Let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(0,6\right) \end{align*}\] and \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(-2,0\right) \end{align*}\] Then \[\begin{align*} Gradient & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{0-6}{-2-0}=\frac{-6}{-2}=3. \end{align*}\] The gradient is 3.Find the gradient of the line joining the two points \(\left(1,3\right)\) and \(\left(4,5\right).\)
Solution:
Let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(1,3\right) \end{align*}\] and \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(4,5\right) \end{align*}\] Then \[\begin{align*} Gradient & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-3}{4-1}=\frac{2}{3}. \end{align*}\] The gradient is \(2/3.\)
See Exercise 2
Equation of a Straight Line
The general equation of a straight line is \[\begin{align*} y & =mx+c \end{align*}\] where \(m\) is the gradient, and \(c\) is the value of the intercept on the \(y\)-axis. The figure below illustrates this.
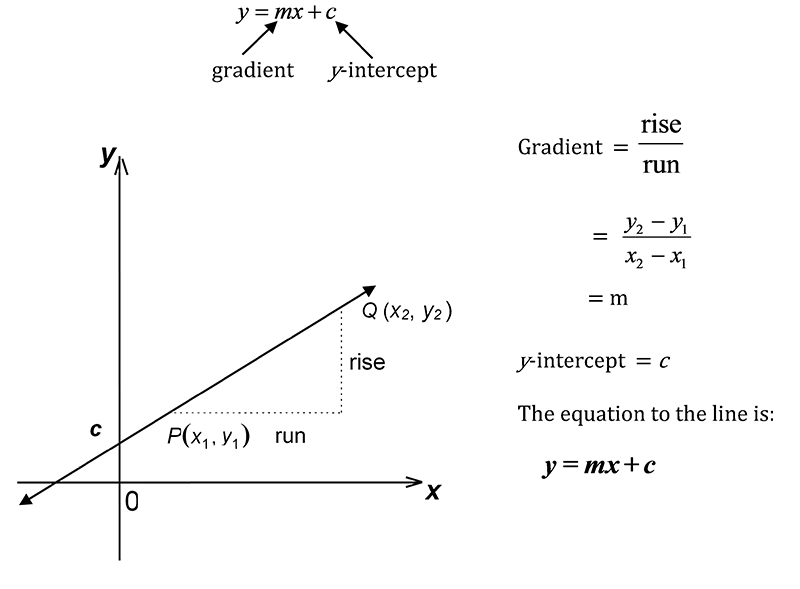
The equation of a straight line can also be written as2 To see this, assume you know a point \(\left(x_{1},y_{1}\right)\) on the line and the gradient \(m\) of the line. Since \(\left(x_{1},y_{1}\right)\) is on the line, it must satisfy the equation \[\begin{align*} y & =mx+c. & \left(1\right) \end{align*}\] and so \[\begin{align*} y_{1} & =mx_{1}+c. & \left(2\right) \end{align*}\] Now subtract \(\left(2\right)\) from \(\left(1\right)\) to get \[\begin{align*} y-y_{1} & =mx+c-\left(mx_{1}+c\right)\\ & =mx-mx_{1}+c-c\\ & =m\left(x-x_{1}\right). \end{align*}\] \[\begin{align*} y-y_{1} & =m(x-x_{1}) \end{align*}\] where \(m\) is the gradient and (\(x_{1},y_{1}\)) is a point on the line. This is called point-slope form because it assumes you know
A point on the line \(\left(x_{1},y_{1}\right)\) and
The gradient \(m\) of the line.
Some Properties of Linear Graphs
A line that slopes up and to the right has a positive gradient.
A line that slopes up and to the left has a negative gradient.
Parallel lines have the same gradient.
The gradients of two mutually perpendicular lines multiply to \(-1.\)
A line parallel to the x – axis has a gradient of \(0\).
A line parallel to the y – axis; the gradient is undefined.
Examples
Example 1: Find the gradient and the equation of the straight line below:

Solution:
First note that the graph has a positive gradient.3 Because it slopes up (increases) as you move to the right. You don’t have to write this but it is a good check to have in mind. If you calculate a negative gradient, you know something has gone wrong. Let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(1,3\right) \end{align*}\] and \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(3,7\right). \end{align*}\] Then the gradient \(m\) is given by \[\begin{align*} m & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\ & =\frac{7-3}{3-1}\\ & =\frac{4}{2}\\ & =2. \end{align*}\] So the gradient \(m=2.\) From the graph we see the \(y\)-intercept is \(1.\) That is, \(c=1.\) Now we can substitute in the equation for a line4 The equation for a line is \[\begin{align*} y & =mx+c. \end{align*}\] to get \[\begin{align*} y & =2x+1. \end{align*}\] The equation for the line is \(y=2x+1.\)
Example 2: Find the gradient and the equation of the straight line below:

Solution:
First note that the graph has a negative gradient.5 Because it slopes down (decreases) as you move to the right. You don’t have to write this but it is a good check to have in mind. If you calculate a positive gradient, you know something has gone wrong.
Let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(0,4\right) \end{align*}\] and \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(6,0\right) \end{align*}\] Then the gradient \(m\) is given by \[\begin{align*} m & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\ & =\frac{0-4}{6-0}\\ & =-\frac{2}{3}. \end{align*}\] The \(y\)-intercept is at \(\left(0,4\right)\) and so \(c=4.\) Hence the equation of the line is \(y=-\frac{2}{3}x+4.\) This is a correct answer but the fraction makes it look a bit ugly. We can multiply both sides by \(3\) to get rid of the fraction. The equation then becomes: \(3y=-2x+12\) or \(3y+2x=12.\)
Example 3: Sketch the function \(2y=x-6\) and state the gradient of the straight line.
Solution:
First find the \(x\) and \(y\) intercepts. For the \(x\)-intercept, set \(y=0\) then \[\begin{align*} 0 & =x-6\\ \text{and }x & =6. \end{align*}\] Hence the \(x\)-intercept is at \(\left(6,0\right)\).
For the \(y\)-intercept, set \(x=0\) then \[\begin{align*} 2y & =-6\\ \text{and }y & =-3. \end{align*}\] Hence the \(y\)-intercept is at \(\left(0,-3\right).\)
Now draw a line between these two points as shown below:
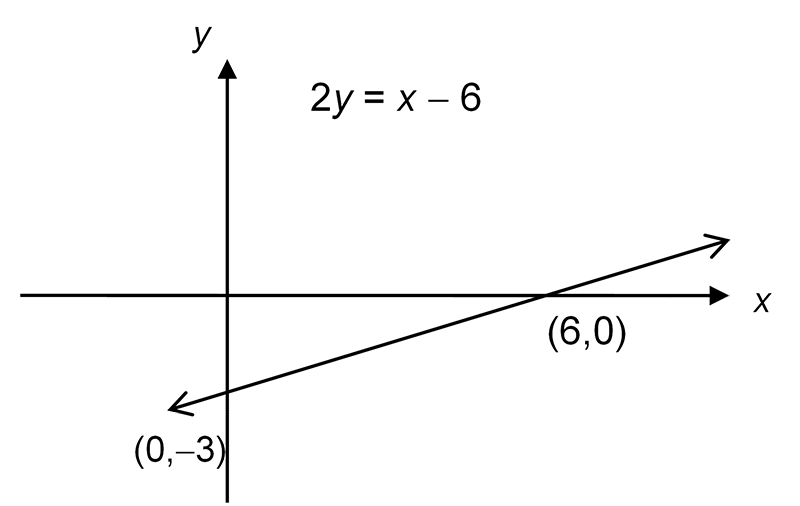
To find the gradient, let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(0,-3\right) \end{align*}\] and \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(6,0\right). \end{align*}\] Then the gradient \(m\) is given by \[\begin{align*} m & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\ & \frac{0-\left(-3\right)}{6-0}\\ & =\frac{3}{6}\\ & =\frac{1}{2}. \end{align*}\] Alternatively, to find the gradient divide both sides of the equation by \(2\) to get \[\begin{align*} 2y & =x-6\\ y & =\frac{1}{2}x-3. \end{align*}\] This is in the standard form \(y=mx+c\) and we see that the gradient \(m=1/2\) as before.
Example 4: Sketch the graph of \(3y+2x=0\) and state the gradient of the straight line.
Solution:
First find the intercepts. For the \(x\)-intercept \(y=0\). Substituting in the equation we get \[\begin{align*} 2x & =0\\ x & =0 \end{align*}\] and the \(x\)-intercept is at \(\left(0,0\right).\) For the \(y\)-intercept, \(x=0.\) Substituting in the equation we get \[\begin{align*} 3y & =0\\ y & =0 \end{align*}\] and the \(y\)-intercept is at \(\left(0,0\right).\) But this means the \(x\)-intercept is equal to the \(y\)-intercept. This is because the line passes through the origin \(\left(0,0\right)\).6 We could have seen this by considering the equation of the line: \(3y+2x=0.\) Rearranging the equation and dividing by \(3\) we get \[\begin{align*} 3y+2x & =0\\ 3y & =-2x\\ y & =-\frac{2}{3}x. \end{align*}\] Comparing this to the standard form \(y=mx+c\) we see that \(m=-2/3\) and \(c=0.\) That is the \(y\)-intercept is at \(\left(0,0\right).\)
So far we know the graph goes through \(\left(0,0\right).\) To sketch its graph we need another point. To find another point on the line, pick any value of \(x\) (other than \(0\)). Let’s take \(x=3\) then substituting into the equation we have \[\begin{align*} 3y+2\left(3\right) & =0\\ 3y & =-6\\ y & =-2 \end{align*}\] so the point \(\left(3,-2\right)\) is on the graph.
To sketch the graph, we plot the points \(\left(0,0\right)\) and \(\left(3,-2\right)\) and draw a line through them as shown below.
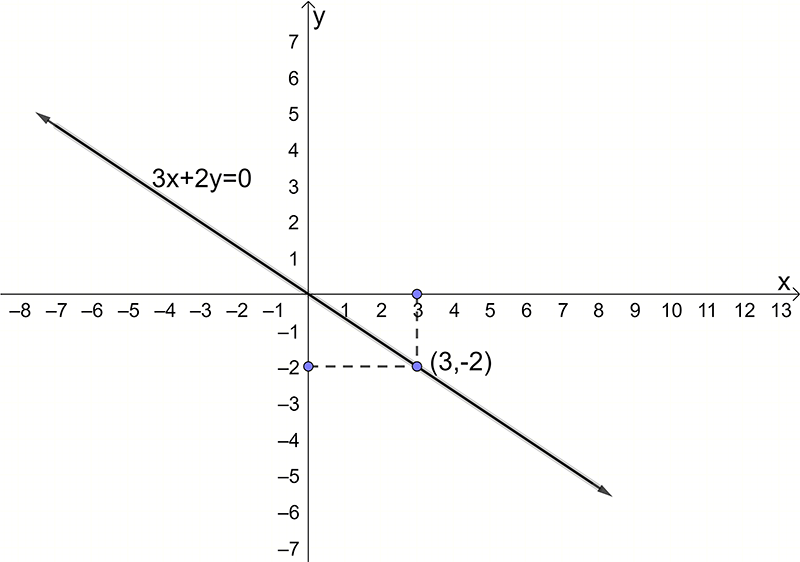
To find the gradient, rearrange the equation to the form of \(y=mx+c\):
\[\begin{align*} 3y+2x & =0\\ y & =-\frac{2}{3}x \end{align*}\]
The gradient of the line is \(-\frac{2}{3}\).
Example 5: Find the equation of the line that passes through the points \(\left(-1,3\right)\) and \(\left(2,0\right)\).
Solution:
First find the gradient \(m.\) Let \[\begin{align*} \left(x_{1},y_{1}\right) & =\left(-1,3\right) \end{align*}\] and \[\begin{align*} \left(x_{2},y_{2}\right) & =\left(2,0\right). \end{align*}\] Then the gradient \(m\) is given by \[\begin{align*} m & =\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\ & \frac{0-3}{2-\left(-1\right)}\\ & =\frac{-3}{3}\\ & =-1. \end{align*}\]
The equation to our line is \(y=-x+c\). We need to find \(c.\) To find \(c\) substitute either of the points on the line into the equation for the line. Using the point \(\left(-1,3\right)\) we obtain \[\begin{align*} y & =-x+c\\ 3 & =-\left(-1\right)+c\\ c & =3-1\\ & =2. \end{align*}\]
The equation to the line is \(y=-x+2\).
Example 6: Find the equation of the line that passes through the point \(\left(3,4\right)\) and parallel to the line \(y=-2x+7.\) Give your answer in point slope form.
Solution:
The point-slope form of the equation to a straight line is \[\begin{align*} y-y_{1} & =m\left(x-x_{1}\right). \end{align*}\]
The gradient of the line \(y=-2x+7\) is \(-2\), so \(m=-2\).
The point on the line is (\(3,4\)) so \(x_{1}=3\) and \(y_{1}=4\).
Substituting in the point slope equation gives: \[\begin{align*} y-y_{1} & =m\left(x-x_{1}\right)\\ y-4 & =-2\left(x-3\right). \end{align*}\]
The equation to the line is \(y-4=-2(x-3)\).
See Exercise 3
Exercise 1
Sketch the graphs of the following equations.
\[\begin{array}{lllllllclc} \textrm{(a)} & y=4x+3 & & & \textrm{(b)} & 2y=-x+6 & & & \textrm{(c)} & 3y+2x=9\\ \textrm{(d)} & y=2x & & & \textrm{(e)} & y=7 & & & \textrm{(f)} & 2y+x=0 \end{array}\]
- \(\textrm{a. }y=4x+3\)
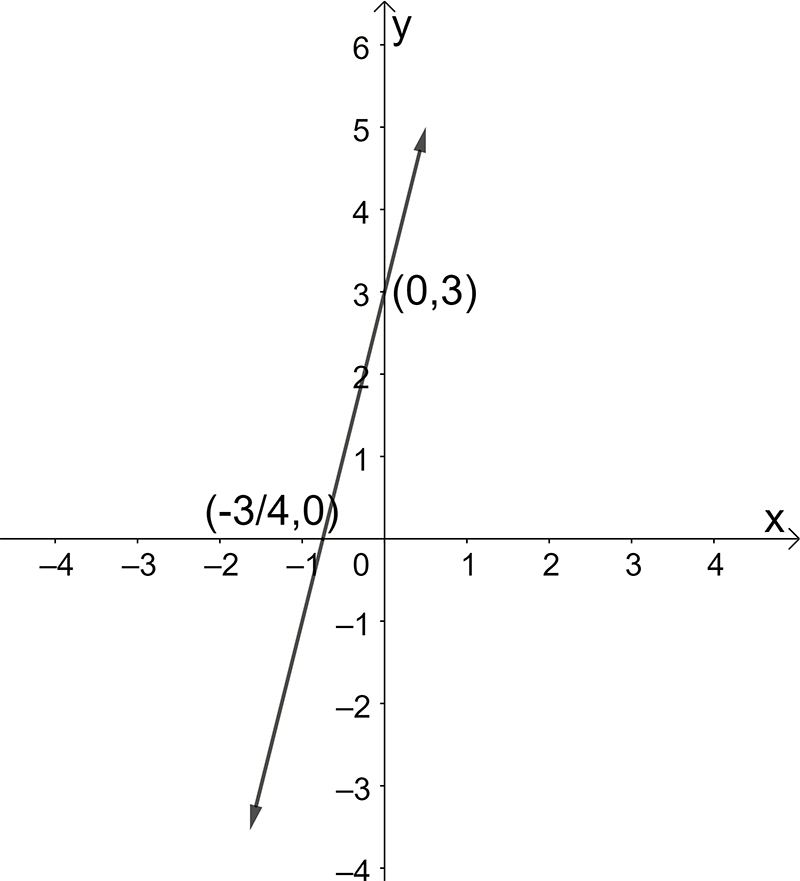
- \(2y=-x+6\)
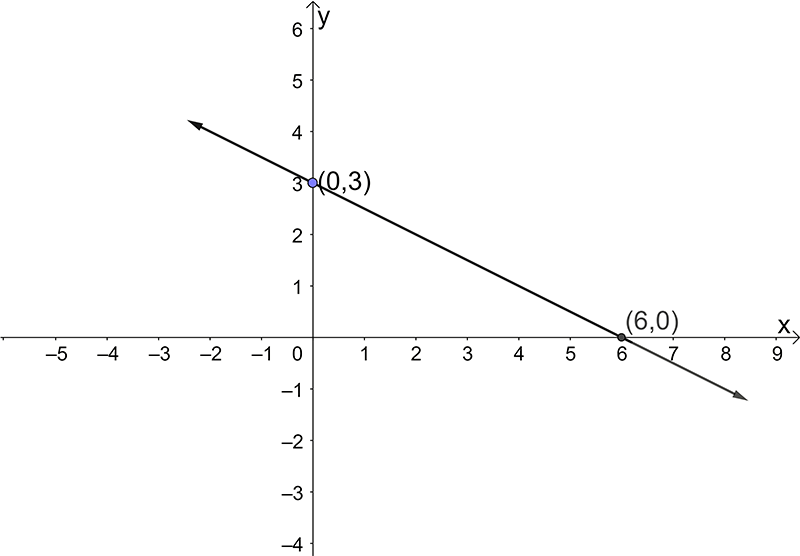
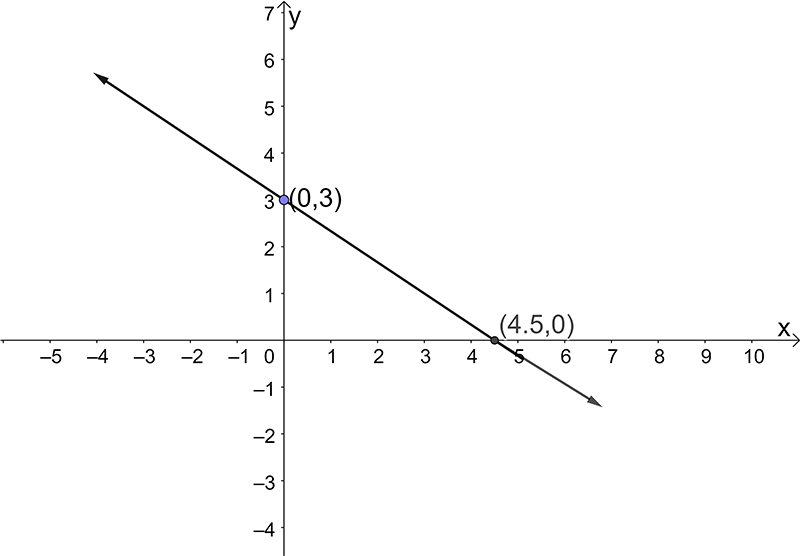
- \(3y+2x=9\)
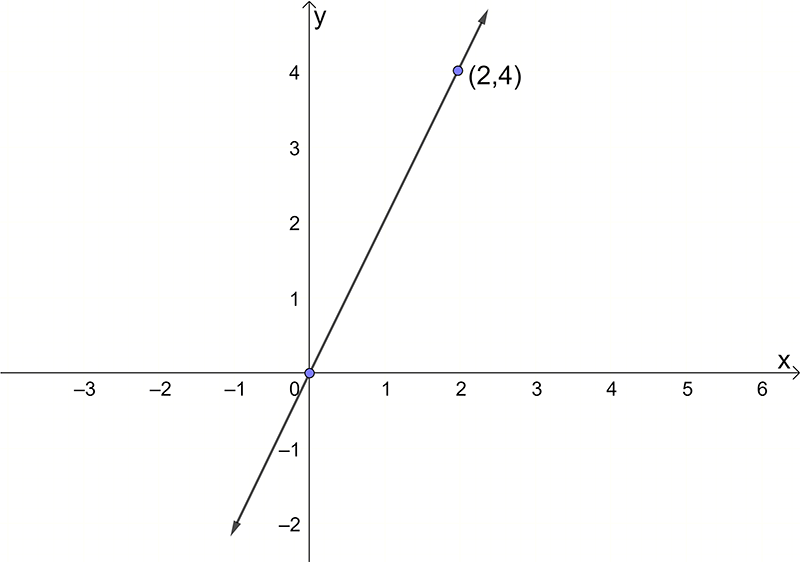
- \(y=2x\)
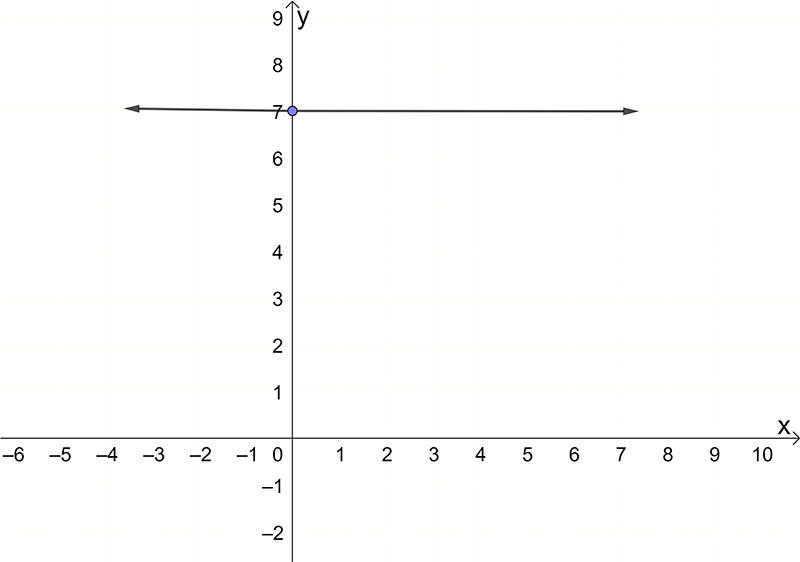
- \(y=7\)
- \(2y+x=0\)
Exercise 2
Find the gradient of the following straight lines.
\[\begin{array}{lllllllclc} \textrm{(a)} & y=-5x & & & \textrm{(b)} & 2y=6x+9 & & & \textrm{(c)} & 2x-3y=0\\ \textrm{(d)} & 3y+2x-2=0 & & & \textrm{(e)} & 5y=8 & & & \textrm{(f)} & x=-2 \end{array}\]
\(\begin{aligned}\begin{array}{llll} 2. & \left(\text{a}\right)\,-5 & \left(\text{b}\right)\,3 & \left(\text{c}\right)\,2/3\\ \end{array}\end{aligned}\)
Exercise 3
Find the equation of the straight lines below

- Find the equation, in slope-point form, of the line with a gradient of \(3\), passing through the point (\(0,-5\)).
\(\begin{aligned}\begin{array}{llll} 3. & \left(\text{a}\right)\,2y=-x+4 & \left(\text{b}\right)\,y=x+5 & \left(\text{c}\right)\,y+5=3x \end{array}\end{aligned}\)
Download this page, FG7 Linear graphs (PDF 2.57MB)
What's next... FG8 Quadratic graphs
