FG1 Functions and relations
A relation is a set of ordered pairs.
Relations
A relation is a set of ordered pairs. For example \((1,2),(2,6),(3,4),(x,y)\) are ordered pairs and \(\left\{ (1,2),(2,6),(3,4),(x,y)\right\}\)is a relation.
The domain of a relation is the set of first elements or the \(x\)-values of the ordered pairs.
For the above ordered pairs the domain, dom = \(\left\{ 1,2,3,x\right\}\).
The range of a relation is the set of second elements or the \(y\)-values of the ordered pairs. For the above ordered pairs the range, ran = \(\left\{ 2,4,6,y\right\}\).
There is often a rule that links the domain and range.
For example: 1 The symbol \(\in\) means “is in” or “is an element of” , the symbol \(\mathbb{R}\) stands for the set of real numbers. The expression \[\begin{align*} x\in & \mathbb{R} \end{align*}\] means that “x is an element of the set of real numbers”. That is, \(x\) is a real number. \[ S=\left\{ \left(x,y\right):y>x,\,x\in\mathbb{R}\right\} \]
This relation, called S, consists of the set of all ordered pairs (\(x\) and \(y\)), where the \(y\) value is greater than the \(x\) value and where \(x\) must be a real number.
Note that a relation is defined by its rule (in this case \(y>x\)) and its domain (in this case \(x\in\mathbb{R}\)).2 If the domain is not given then we assume the largest possible domain.
Example 1
Sketch the graph of the following relation and state the domain and range:
\[ \left\{ \left(x,y\right):y=x^{2}\right\} . \]
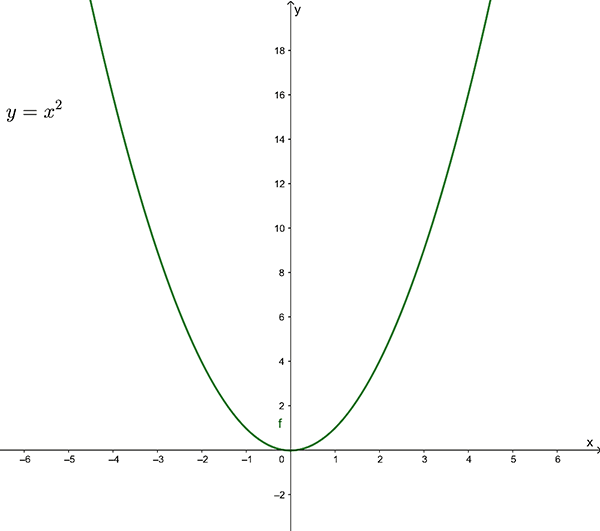
In this example the rule joining the set of ordered pairs (\(x,y\)) is \(y=x^{2}\).
\(x\) can be any real number. Domain is \(\mathbb{R}.\)
\(y\) must be greater than or equal to zero. Range is \(\left\{ y:y\geq0\right\}\)
Example 2
Sketch the graph of \(x^{2}+y^{2}=4\). State the Domain and Range of this relation.
In this example the rule joining the set of ordered pairs (\(x,y\)) is \(x^{2}+y^{2}=4\).
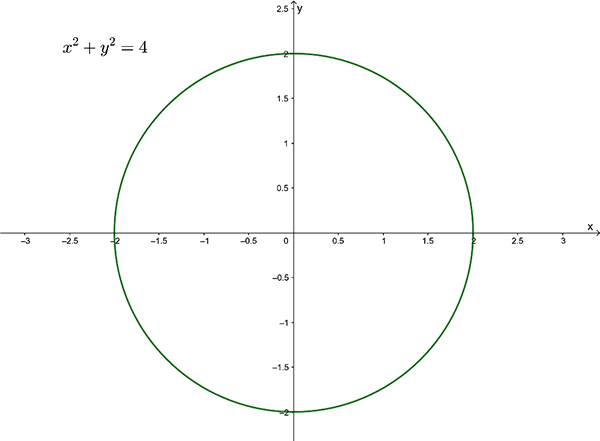
From the graph it can be seen that the domain is \(\left\{ x:-2\leq x\leq2\right\}\) and the range is \(\left\{ y:-2\leq y\leq2\right\} .\)
Example 3
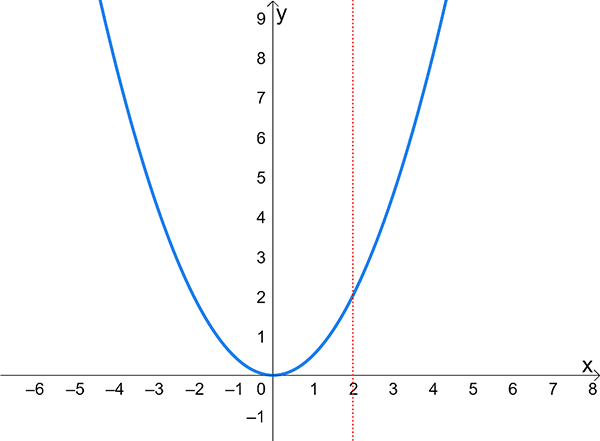
Sketch the graph of \(\left\{ (x,y):2x+3y=6,x\geq0\right\}\) and state the domain and range of this relation.
In this example the rule joining the set of ordered pairs \((x,y)\) is \(2x+3y=6\).
The restriction \(x\geq0\) is placed on the domain.
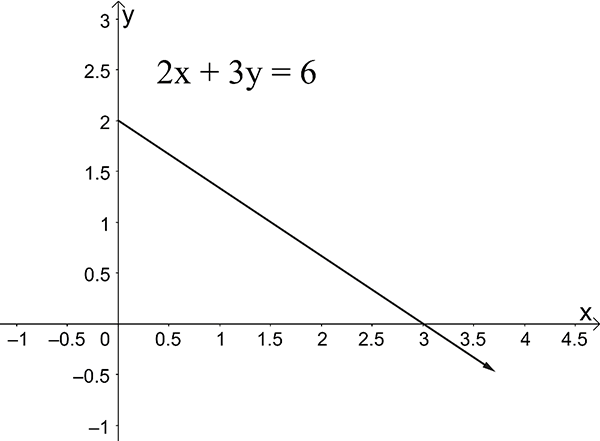
The domain is \(\left\{ x:x\geq0\right\}\) as is specified in the statement of the relation.
The range is \(\left\{ y:y\leq2\right\}\) as can be seen from the graph.
The rule of a relation may be thought of as: \(\textrm{DOMAIN$\rightarrow\textrm{RULE$\rightarrow\textrm{RANGE.}$ }$ }\) Values taken from the domain produce values for the range, after passing through the rule that defines the relation.3 See Exercise 1
Functions
From some of the previous examples it can be seen that some values in the domain (\(x\) values) may have many, even an infinite number of corresponding values in the range (\(y\) values).
A function is a special type of relation. Each point in the domain of a function has a unique value in the range. Every value of \(x\) may have only one value of \(y\) .
Examples
The relation \(\left\{ (-1,2),(-1,4),(1,6),(2,8),(3,10)\right\}\) is not a function because the value \(x=-1\) has two corresponding \(y\) values \((2\textrm{ and}\) \(4)\).
The relation \(\left\{ (-1,1),(0,2),(1,3),(2,5),(3,7)\right\}\) is a function because for each \(x\) value there is only one corresponding \(y\) value.
\(F=\left\{ \left(x,y\right):y=\sin x,x\in R\right\}\)
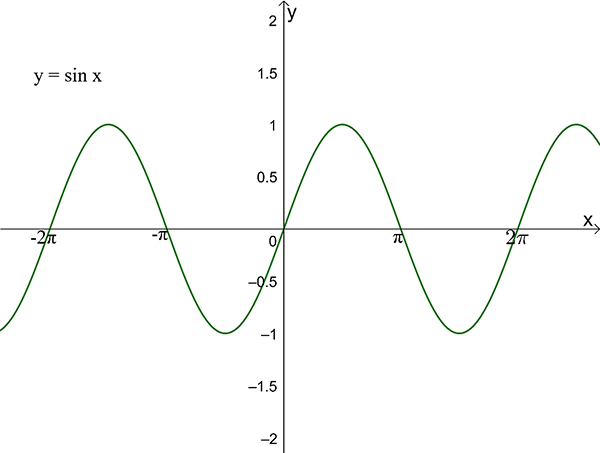
If we choose any possible value of \(x,\) there exists only one corresponding value of \(y\). Therefore, the relation \(F\) is a function.
Another way of writing this function is with mapping notation.
\[ f:X\rightarrow Y,\textrm{where $f(x)=\sin x.$ } \]
(The domain, \(X\), is mapped onto the range, \(Y\), using the rule \(f(x)=\sin x\) )
If only the rule is given then we assume that the domain is \(\mathbb{R}\).
Vertical Line Test
When relations are represented graphically, a vertical line test may be applied to decide if they are functions.
If a vertical line crosses the graph more than once, then it is not a function, as an \(x\) value has more than one \(y\) value.
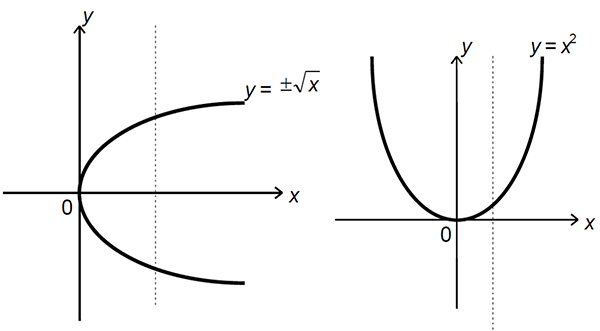
The graph on the left is not a function (the vertical line crosses the graph more than once), the graph on the right is a function (vertical line only crosses the graph once). 4 See Exercise 2
Implied Domain
If only the rule of the function is given, then we assume that the domain is \(\mathbb{R}\) (the set of real numbers) unless otherwise defined implicitly by the function.
Examples
If a function involves a square root, the domain, in the real number system, is restricted to those values of \(x\) that result in a non-negative number under the square root sign.
So, the domain of the function \(y=+\sqrt{x-4}\) is restricted such that \(x-4\geq0\) ; the domain is \(\left\{ x:x\geq4\right\}\).The domain of the function \(y=+\sqrt{9-x^{2}}\) is restricted such that \(9-x^{2}\geq0\) ; the domain is \(\left\{ x:-3\leq x\leq3\right\}\).
If the function involves a fraction, the value in the denominator must not equal zero.
So, the domain of the function \(y=\dfrac{3}{x+5}\) is restricted such that \(x+5\neq0\) ; the domain is \(\left\{ x:x\neq-5\right\}\).5 The domain may be written as \[\begin{align*} \left\{ x:x\in\mathbb{R}\setminus\left\{ -5\right\} \right\} . \end{align*}\] Here \(\mathbb{R}\setminus\left\{ -5\right\}\) is the set of real numbers excluding \(-5\).The domain of the function \(y=\dfrac{3}{2x-8}\) is restricted such that 2\(x-8\neq0\) ; the domain is \(\left\{ x:x\neq4\right\}\) or \(\left\{ x:x\in\mathbb{R}\setminus\left\{ 4\right\} \right\}\). 6 See Exercise 3
Exercises
Exercise 1.
State the domain and range of the following relations
\(\left\{ \left(-2,1\right),\left(0,2\right),\left(2,5\right),\left(2,7\right),\left(3,9\right)\right\}\)
\(\left\{ \left(4,1\right),\left(5,2\right),\left(6,3\right)\right\}\)
\(\left\{ \left(x,y\right):x^{2}+y^{2}=25\right\}\)
\(\left\{ \left(x,y\right):2y=6-5x,x\geq2\right\}\)
Exercise 2.
Which of the following relations are functions?
\(\left\{ \left(x,y\right):y=2x+4\right\}\)
\(\left\{ \left(x,y\right):y=4-x^{2}\right\}\)
\(\left\{ \left(x,y\right):x^{2}+y^{2}=36\right\}\)
\(\left\{ \left(x,y\right):y=7\right\}\)
\(\left\{ \left(x,y\right):x=-2\right\}\)
\(\left\{ \left(x,y\right):y=-\sqrt{4-x^{2}}\right\}\)
Exercise 3.
State the domain of the following functions.
\(\left\{ \left(x,y\right):y=x+2\right\}\)
\(\left\{ \left(x,y\right):y=4-x^{2}\right\}\)
\(\left\{ \left(x,y\right):y=+\sqrt{4-x}\right\}\)
\(\left\{ \left(x,y\right):y=\dfrac{3}{x+2}\right\}\)
\(\left\{ \left(x,y\right):y=\dfrac{5}{\sqrt{x-7}}\right\}\)
\(\left\{ \left(x,y\right):y=\dfrac{1}{x+2}-\dfrac{3}{x-4}\right\}\)
Answers
Exercise 1.
domain = \(\left\{ -2,0,2,3\right\}\) range = \(\left\{ 1,2,5,7,9\right\}\)
domain = \(\left\{ 4,5,6\right\}\) range = \(\left\{ 1,2,3\right\}\)
domain = \(\left\{ x:-5\leq x\leq5\right\}\) range = \(\left\{ y:-5\leq y\leq5\right\}\)
domain = \(\left\{ x:x\geq2\right\}\) range = \(\left\{ y:y\leq-2\right\}\)
Exercise 2.
(a), (b), (d), (f)
Exercise 3.
State the domain of the following functions.
\(\mathbb{R}\)
\(\mathbb{R}\)
\(\left\{ x:x\leq4\right\}\)
\(\left\{ x:x\neq-2\right\}\)
\(\left\{ x:x>7\right\}\)
\(\left\{ x:x\in\mathbb{R}\setminus\left\{ -4\right\} \right\}\)
Download this page, FG1 Functions and Graphs (PDF 399 KB)
What's next... FG2 Interval notation
