ES4 Quadratic formula
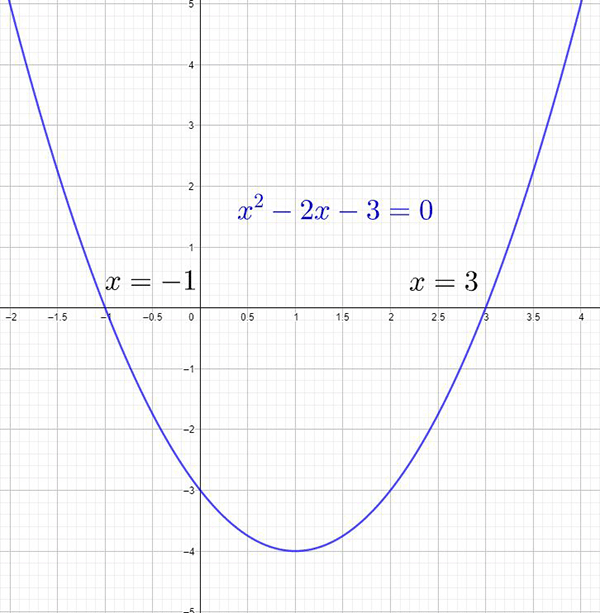
The solutions to any quadratic equation can be found by substituting the values a, b, c into the quadratic formula.
The solutions to any quadratic equation \(ax^{2}+bx+c=0\) can be found by substituting the values \(a,b,c\) into the quadratic formula:
\[ x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}. \] Solutions may be real or complex numbers.
In this module we only consider real solutions.
Example 1
Solve the equation: \[ x^{2}-5x+4=0. \]
Solution:
We have1 Note that \(x^{2}=1\times x^{2}\) and so \(a=1\) . \(a=1,\ \,b=-5\) and \(c=4.\) Substituting into the formula we get: \[\begin{align*} x & =\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\\ & =\frac{-(-5)\pm\sqrt{(-5)^{2}-4(1)(4)}}{2(1)}\\ & =\frac{5\pm\sqrt{25-16}}{2}\\ & =\frac{5\pm\sqrt{9}}{2}\\ & =\frac{5\pm3}{2}\\ & =\frac{5+3}{2}\ \textrm{ or }\ \frac{5-3}{2}\\ & =\frac{8}{2}\ \textrm{ or }\ \frac{2}{2}\\ & =4\ \textrm{ or }\ 1. \end{align*}\] The solution is \(x=1\) or \(x=4\).
Example 2
Solve the equation: \[ x^{2}+x+10=0. \]
Solution:
We have \(a=1,\,b=1\) and \(c=10.\) Substituting into the formula we get: \[\begin{align*} x & =\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\\ & =\frac{-1\pm\sqrt{1^{2}-4(1)(10)}}{2(1)}\\ & =\frac{-1\pm\sqrt{1-40}}{2}\\ & =\frac{-1\pm\sqrt{-39}}{2}. \end{align*}\] Since the \(\sqrt{-39}\) does not exist the equation has no solution.2 There is a solution if we use complex numbers but we are looking for real solutions.
Discriminant
The part of the quadratic formula which is under the radical sign (\(b^{2}-4ac)\) is called the discriminant. Its value determines the number of solutions and whether they will be rational or irrational.
- If \(b^{2}-4ac<0\) there are no (real) solutions. This means the graph of \(y=ax^{2}+bx+c\) doesn’t touch or cut the \(x\)-axis.
- If \(b^{2}-4ac=0\) there is one solution. This means the graph of \(y=ax^{2}+bx+c\) touches the \(x\)-axis at this value of \(x\).
- If \(b^{2}-4ac>0\) there are two solutions. This means the graph of \(y=ax^{2}+bx+c\) cuts the \(x\)-axis at these values of \(x\).
- If \(b^{2}-4ac\quad\)is a perfect square the solutions will be rational .
3 A number is a perfect square if its square root is an integer. Integers are whole numbers: \(\ldots,-2,-1,0,1,2,\ldots\)
4 A rational number can be expressed as a fraction \(p/q\) where \(p\) and \(q\neq0\) are integers.
Exercise
Solve the following quadratic equations for real solutions (if possible):
\[\begin{array}{llllllll} \textrm{1.} & x-4x-7=0 & & \textrm{} & & \textrm{} & \textrm{2.} & x^{2}-2x-2=0\\ \\ 3. & x^{2}+6x-9=0 & & & & & \textrm{4.} & x^{2}-x-7=0\\ \\ 5. & 4x^{2}-12x+6=0 & & & & & \textrm{6.} & 2x^{2}+x-2=0\\ \\ \textrm{7.} & x^{2}-4x+2=0 & & & & & \textrm{8.} & 2x^{2}-3x+2=0\\ \\ \textrm{9.} & 3x^{2}+5x-7=0 & & & & & \textrm{10.} & 3x^{2}=x+1\\ \\ \textrm{11.} & 4x^{2}+x+3=0 & & & & & \textrm{12.} & \frac{3x+1}{2}=\frac{x+1}{x} \end{array}\]
\[\begin{array}{llllllll} \textrm{1.} & x=\frac{4\pm\sqrt{44}}{2}=2\pm\sqrt{11} & & \textrm{} & & \textrm{} & \textrm{2.} & x=\frac{2\pm\sqrt{12}}{2}=1\pm\sqrt{3}\\ \\ \textrm{3.} & x=\frac{-6\pm\sqrt{72}}{2}=-3\pm3\sqrt{2} & & & & & 4. & x=\frac{1\pm\sqrt{29}}{2}\\ \\ 5. & x=\frac{12\pm\sqrt{48}}{8}=\frac{3\pm\sqrt{3}}{2} & & & & & \textrm{6.} & x=\frac{-1\pm\sqrt{17}}{4}\\ \\ \textrm{7.} & x=\frac{4\pm\sqrt{8}}{2}=2\pm\sqrt{2} & & & & & \textrm{8.} & no\:solution\\ \\ \textrm{9.} & x=\frac{-5\pm\sqrt{109}}{6} & & & & & \textrm{10.} & x=\frac{1\pm\sqrt{13}}{6}\\ \\ \textrm{11.} & no\:solution & & & & & \textrm{12.} & x=-\frac{2}{3},\quad x=1 \end{array}\]
Download this page, ES4 The Quadratic Formula (PDF 227 KB)
What's next... ES5 Cubic equations, polynomial long division
