ES2 Simultaneous equations
Two equations in two variables are said to be simultaneous if both must be considered at the same time.
Two equations in two variables are said to be simultaneous if both must be considered at the same time. An ordered pair \(\left(x,y\right)\) which satisfies both equations is said to be a solution for the simultaneous equations. Three methods for solving a pair of simultaneous equations using algebra are:
\(\text{1. elimination}\)
\(\text{2. substitution}\)
\(\text{3. graphical.}\)
Each method is discussed in this module.
Elimination Method
In the elimination method we manipulate the equations so that one of the variables has coefficients that are equal or opposite in sign. The manipulation is multiplication of one or both equations by a constant. Then we add or subtract the equations to eliminate a variable.
Example 1 (Elimination)
Solve the simultaneous equations \(x+y=6\) and \(x-y=2\).
Solution: \[\begin{align*} x+y & =6\quad\left(1\right)\quad\text{(number the equations)}\\ x-y & =2\quad\left(2\right)\quad\text{(note the $y$ coefficients are equal and opposite)}\\ 2x & =8\quad\left(1\right)+\left(2\right)\quad\text{(add equations to eliminate $y$ )}\\ x & =4.\\ \textrm{Substitute $x=4$ } & \textrm{back into equation $\left(1\right)$ or $\left(2\right)$ to solve for }y\\ 4+y & =6\quad\text{(using $\left(1\right))$ }\\ y & =2. \end{align*}\]
The solution is (\(4,2\)).
We can check the solution by substituting in the original equations. Substituting \(x=4\) and \(y=2\) in \((1)\) gives: \[\begin{align*} \text{LHS} & =x+y\\ & =4+2\\ & =6\\ & =\text{RHS.} \end{align*}\] Substituting \(x=4\) and \(y=2\) in \((2)\) gives: \[\begin{align*} \text{LHS} & =x-y\\ & =4-2\\ & =2\\ & =\text{RHS.} \end{align*}\] Hence our solution is correct.
Example 2 (Elimination)
Solve simultaneously \(3x+2y=10\) and \(4x+3y=13.\)
Solution:
\[\begin{align*} 3x+2y & =10\quad\left(1\right)\quad\text{(number the equations)}\\ 4x+3y & =13\quad\left(2\right) \end{align*}\] In this case we need to manipulate the equations to make the \(x\) or \(y\) coefficients the same or opposite in sign. We will eliminate \(x\) and so multiply equation \(\left(1\right)\) by \(4\) (coefficient of \(x\) in equation \(\left(2\right)\)) and multiply equation \(\left(2\right)\) by \(3\) (the coefficient of \(x\) in equation \(\left(1\right))\) to get:1 To eliminate \(y\) we would multiply equation \(\left(1\right)\) by \(3\) (coefficient of \(y\) in equation \(\left(2\right)\)) and multiply equation \(\left(2\right)\) by \(2\) (the coefficient of \(y\) in equation \(\left(1\right))\) to get: \[\begin{align*} 9x+6y & =30\quad\left(3\right)\\ 8x+6y & =26\quad\left(4\right). \end{align*}\] Then subtracting \(\left(4\right)\) from \(\left(3\right)\) gives \[\begin{align*} x & =4. \end{align*}\] Substituting \(x=4\) into either equation \(\left(1\right)\) or \(\left(2\right)\) gives \(y\).
\[\begin{align*} 12x+8y & =40\quad\left(3\right)\\ 12x+9y & =39\quad\left(4\right). \end{align*}\] Now \(x\) may be eliminated by subtracting equation \(\left(3\right)\) from \(\left(4\right)\):2 We could also subtract equation \(\left(4\right)\) from \(\left(3\right)\) to get \[\begin{align*} -y & =1\\ y & =-1. \end{align*}\] The answer is the same and the order of subtraction doesn’t matter. \[\begin{align*} y & =-1. \end{align*}\] Now substitute this into either equation \(\left(1\right)\) or \(\left(2\right)\). It doesn’t matter which one you use though sometimes one choice is a little easier. In this case we use equation \(\left(1\right)\): \[\begin{align*} 3x+2\left(-1\right) & =10\\ 3x & =10+2\\ x & =4. \end{align*}\] The solution is (\(4,-1\)) and this may be checked by substitution of \(x=4\) and \(y=-1\) into equations \(\left(1\right)\) and \(\left(2\right).\) For equation \(\left(1\right):\) \[\begin{align*} \text{LHS} & =3\left(4\right)+2\left(-1\right)\\ & =12-2\\ & =10\\ & =\text{RHS } \end{align*}\] and for equation \(\left(2\right)\) \[\begin{align*} \text{LHS} & =4\left(4\right)+3\left(-1\right)\\ & =16-3\\ & =13\\ & =\text{RHS } \end{align*}\] so our solution is correct.
Substitution Method
In the substitution method, the simpler equation is transposed to make one of the variables the subject. This variable is then substituted into the second equation to get an equation in one variable which may be solved. Once one variable is known, we can solve for the other variable.
Example 3 (Substitution)
Solve the simultaneous equations \(x+y=6\) and \(x-y=2\).
Solution:
First number the equations. \[\begin{align*} x+y & =6 & \left(1\right)\\ x-y & =2. & \left(2\right) \end{align*}\]
Rearrange \(\left(1\right)\) to make \(x\) the subject:3 Note that you can also make \(y\) the subject and proceed in the same way. From \(\left(1\right)\), \(y=6-x.\) Substituting in \(\left(2\right)\) gives \[\begin{align*} x-\left(6-x\right) & =2\\ -2x & =2+6\\ x & =4 \end{align*}\] and so on. \[\begin{align*} x & =6-y. \end{align*}\] Now substitute in equation \(\left(2\right)\) and solve for \(y:\) \[\begin{align*} 6-y-y & =2\\ -2y & =-4\\ y & =2. \end{align*}\] To find \(x\), substitute \(y=2\) in equation \(\left(1\right)\) or \(\left(2\right)\). We use equation \(\left(1\right)\): \[\begin{align*} x+2 & =6\\ x & =4 \end{align*}\] and the solution is \(x=4\text{ and }y=2\) or \(\left(4,2\right).\) This may be checked by substituting in equations \(\left(1\right)\) and \(\left(2\right).\)
Example 4 (Substitution)
Solve the simultaneous equations \(3x+2y=10\) and \(4x+3y=13\).
Solution:
First number the equations. \[\begin{align*} 3x+2y & =10 & \left(1\right)\\ 4x+3y & =13. & \left(2\right) \end{align*}\]
We can make either \(x\) or \(y\) the subject using equation \(\left(1\right)\) or \(\left(2\right).\) We will make \(y\) the subject. From \(\left(1\right)\), \[\begin{align*} 2y & =10-3x\\ y & =\frac{10-3x}{2} \end{align*}\]
Substitute in \(\left(2\right)\), \[\begin{align*} 4x+3\left(\frac{10-3x}{2}\right) & =13\\ 8x+3\left(10-3x\right) & =26\\ 8x-9x & =26-30\\ -x & =-4\\ x & =4. \end{align*}\] Now substitute for \(x\) in equation \(\left(1\right)\), \[\begin{align*} 3\times4+2y & =10\\ 2y & =-2\\ y & =-1. \end{align*}\] The solution is \(x=4,\ y=-1\) or \(\left(4,-1\right).\) This can be checked by substituting in equations \(\left(1\right)\) and \(\left(2\right).\)
Graphical Method
In the graphical method the straight line graph representing each equation is plotted on the same set of axes. The solution is the point of intersection of the two lines. The graphs must be plotted accurately for this method to give an accurate answer. For this reason it is not usually used unless specifically asked for.
Example 5 (Graphical Method)
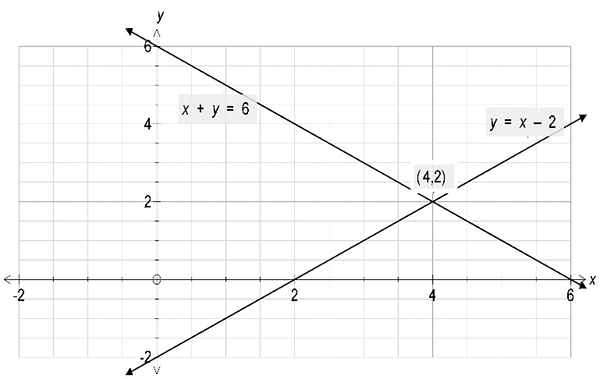
Solve the simultaneous equations \(x+y=6\) and \(x-y=2\) graphically.
Solution:
Graphs representing each linear equation are drawn and the point of intersection is read from the graph.

The solution is (\(4,2\)).
Check by substituting in each equation: \(4+2=6\) and \(4-2=2\).
Equations Without Solutions
Some pairs of equations do not have a solution. Graphically this means that the two lines do not intersect.
Example 6 (No Solution)
Solve the simultaneous equations \(2x-y=6\) and \(-4x+2y=-7\).
Solution:
Number the equations: \[\begin{align*} 2x-y & =6 & \left(1\right)\\ -4x+2y & =-7. & \left(2\right) \end{align*}\] You can use any of the three methods above to try and solve the equations. We will use substitution. From \(\left(1\right)\) we have \[\begin{align*} y & =2x-6. \end{align*}\] Substituting into equation \(\left(2\right)\) gives \[\begin{align*} -4x+2\left(2x-6\right) & =-7\\ -4x+4x-12 & =-7\\ -12 & =-7. \end{align*}\] The last line is impossible and so we conclude no solution exists.
We show the graphs of equation \(\left(1\right)\) and \(\left(2\right)\) below. The two lines are parallel and never intersect, so no solution exists.
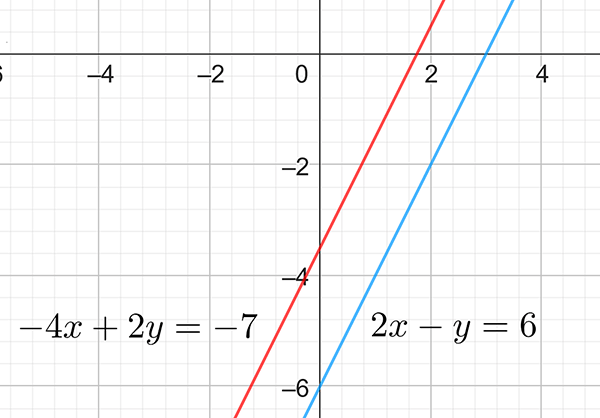
Multiple Solutions
Some pairs of simultaneous equations have multiple solutions. In this case, the equations have the same graph. That is one line lies on the other line.
Example 7 (Multiple Solutions)
Solve \(y=1-3x\) and \(6x=2(1-y)\).
Solution:
Rearrange the equations so that \(x\) and \(y\) are on the same sides and number the equations: \[\begin{align*} 3x+y & =1 & \left(1\right)\\ 6x+2y & =2. & \left(2\right) \end{align*}\] Note that these two lines are the same because \(\left(2\right)=2\times\left(1\right).\) Consequently they have the same graph and there are multiple values of \(x\) and \(y\) that satisfy them. For example, setting \(x=0\) in equation \(\left(1\right)\) gives \(y=1\) so \(\left(0,1\right)\) is a solution. Setting \(y=0\) in equation \(\left(1\right)\) gives \(x=1/3\) and so \(\left(1/3,0\right)\) is also a solution. In fact there are an infinite number of solutions, each corresponding to a point on the line \(3x+y=1.\)
Exercise 1
Solve simultaneously using either the elimination or substitution method:
\(1.\ y=x-3\text{ and $5x-2y=18.$ }\)
\(2.\ y=3x+4\text{ and $2x+3y=23.$ }\)
\(3.\ 4x+y=23\ \text{and $x-y=2.$ }\)
\(4.\ -3x+2y=-4\ \text{and $5x-2y=8$ .}\)
\(5.\ 3x-5y=14\ \text{and $2x+y=5.$ }\)
\(6.\ 3x+2y=18\ \text{and $2x-5y=-7$ .}\)
\(1.\ \left(4,1\right)\quad\quad2.\ \left(1,7\right)\qquad3.\ \left(5,3\right)\qquad4.\ \left(2,1\right)\qquad5.\ \left(3,-1\right)\qquad6.\ \left(4,3\right)\)
Exercise 2
Solve the following simultaneous equations graphically.
\(1.\ y=x-3\ \text{and $x+y=5.$ }\)
\(2.\ 5x-y=8\ \text{and $2y-3x=-2.$ }\)
\(3.\ x+y=1\ \text{and $y-2x=7.$ }\)
\(1.\ \left(4,1\right)\qquad2.\ \left(2,2\right)\qquad3.\ \left(-2,3\right)\)
Download this pdf document: ES2 Simultaneous Equations (PDF 247 KB)
What's next... ES3 Quadratic equations
