ES1 Linear equations
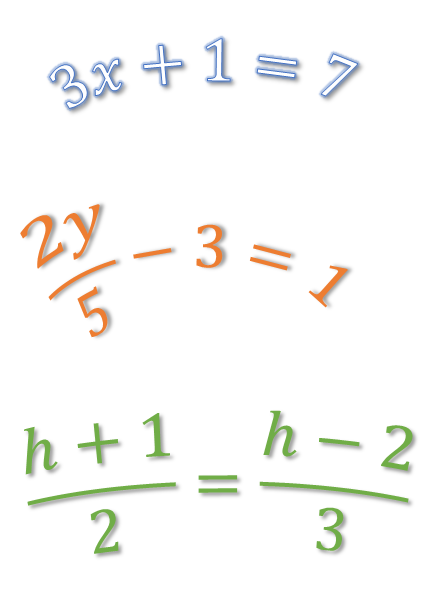
Equations with one variable may be solved using transposition skills to make the variable the subject of the equation.
Solving equations using subtraction; let’s look at a simple equation, X plus three equals seven. So we’re saying what number instead of X which, when added to three, gives us seven. Well obviously the answer is four because four plus three equals seven. An equation is like a balance, the numbers on the left hand side must balance the numbers on the right hand side. But let’s do this another way, let’s get X by itself, in other words we’re doing it mathematically. To do this we subtract the three from the left hand side to isolate the X, so now the left hand side is X plus three minus three which gives us X. Let’s bring in the right hand side, but remember we have to keep the equation balanced, in other words X plus three minus three on the left hand side is equal to seven minus three on the right hand side. You see how the minus three undoes the plus three, so on the left hand side we’ve got X and the right hand side we’ve got four. Notice that the three has been subtracted from both sides, in other words what we do to one side we must do to the other.
So the rule is that the opposite or inverse operation to plus is minus. In other words subtracting undoes adding. Let’s solve an equation using addition. So we’ll start with Y minus six equals 13, so we’re saying what number instead of Y which when added to minus six gives us 13. Well the answer is 19 because 19 take away six equals 13. Again notice the balancing act, 19 minus six on the left hand side is equal to 13 on the right hand side. But let’s do this mathematically. Let’s get Y by itself and to do this we need to add the six from the left hand side to isolate the Y, remember we had to subtract the number with the previous problem, so the left hand side is now Y minus six plus six, which gives us Y, that’s the left hand side. What about the right hand side. Well what we do to one side we do to the other so Y minus six plus six is equal to 13 plus six, notice plus six undoes minus six. In other words Y is equal to 19. Notice again that the six has been added to both sides, so the rule here is that the opposite or inverse operation to minus is plus, in other words adding undoes subtracting.
Let’s solve an equation using division. Let’s look at the equation four K equals 12. Remember four K means four times K, so we’re saying what number instead of K which when multiplied by four gives us 12, well three because four times three is equal to 12, so we have 12 equals 12, our balancing act again. But let’s do this another more mathematical way, let’s get that K by itself and to do this we divide by four on the left hand side to isolate the K. To balance this we must do the same thing on the right hand side, so here we have the left hand side which is four K divided by four, the right hand side we must divide that by four too, so it’s 12 divided by four, there’s the calculation where we’re dividing by four and so we’ve got 12 divided by four is equal to three. Notice this time I’ve just checked the solution to this equation, in other words if K equals three and we substitute four K into the original equation, four times three is equal to 12. So the rule here is that the opposite or inverse operation to multiplication is division. In other words dividing undoes multiplying.
Let’s solve an equation using multiplication. Now here we have an equation M divided by four is equal to minus five, in other words what number instead of M which when divided by four gives us minus five. This one isn’t so easy to work out so we have to use the following rule, in other words let’s use a little bit of mathematics. What we’re doing here is multiplying both sides by four, so M over four times four over one, notice how the fours cancel, is equal to minus five times four over one, or four. In other words minus five times four is minus 20. So let’s check the solution. If the answer is minus 20 then minus 20 divided by four is equal to minus five. So the rule here, for multiplication, is that the opposite or inverse operation to division is multiplication, multiplying undoes dividing.
Now let’s move on to more complicated operations where we have more than one. For instance, let’s look at the equation two P plus five equals seven. The unknown value P is multiplied by two and then five is added to obtain the answer of seven. To find P we undo two P plus five in the reverse order to which it was built up. In other words we subtract five first and then divide by two, which is the opposite to what we did in getting from two P plus five to seven. So let’s subtract five first, two P plus five minus five equals seven minus five, which gives us two. Then let’s divide by two, notice we’re doing it on both sides of the equation, two times P over two equals two over two, the right hand side is now one because we cancelled the two top and bottom, so two P equals two then P equals one.
So let’s look at another equation, but this time it’s a division equation for starters, three X minus one divided by two is equal to one. In order to solve the equation the operations is to build up the equation must be undone in the reserve order. In other words we start by dividing by two and then we add the one. Let’s look at this in more detail. Three X minus one divided by two, let’s multiply both sides by two to get rid of the two on the bottom of the fraction on the left hand side so we end up with three X minus one equals two. Now let’s get rid of the minus one on the left hand side, so three X minus one plus one equals two plus one, notice we’re doing the same operation on both left and right hand sides of the equation. That leaves us with three X equals three here, so the final step is to remove the three on the left hand side and because we have three times X we must divide by three so three X over three equals three over three. Notice the three cancels out and we’re left with X equals one.
So when we solve equations using more than one operation we first of all look at how the operation was built up, then we solve the equation by undoing it in the reverse order to which it was built up. Now go to the exercise sheet and have a go at the problems for yourself. Thank you.
A linear equation has one unknown variable and may be solved by transposing the equation to make the variable the subject of the equation. For example, the equation \[\begin{align*} 3\left(2x-7\right) & =-15 \end{align*}\] may be transposed to get \[\begin{align*} x & =6. \end{align*}\] Transposition involves changing the equation via operations like addition, subtraction, multiplication and division. This module discusses techniques for solving linear equations by transposition.
Simple Equations
The essential point is that in solving an equation, what you do to one side must be done to the other side.
If you add, subtract, multiply or divide one side of the equation by a number you must do the same to the other side. This preserves equality.
Example 1
Solve \(m+4=-2\).
Solution: We want to make \(m\) the subject of the equation. 1 When a variable is the only term on one side of the equal sign we call it the subject. For example the formula for the area of a circle is \[\begin{align*} A & =\pi r^{2}. \end{align*}\] In this case the variable \(A\) is the subject. \[\begin{align*} m+4 & =-2. \end{align*}\] To get \(m\) on its own we need to take \(4\) from both sides to get: 2 Remember that what you do to one side of an equation must be done to the other side to preserve equality. \[\begin{align*} m+4-4 & =-2-4\\ m & =-6. \end{align*}\] The solution is \(m=4.\) Note that you can always check your solution by substituting your answer into the original equation. In this case3 LHS and RHS are abbreviations for left hand side and right hand side respectively. \[\begin{align*} \text{LHS} & =m+4\\ & =-6+4\\ & =-2\\ & =\text{RHS} \end{align*}\] and so our solution is correct.
Example 2
Solve \(p-2=5\).
Solution: We want to make \(p\) the subject. To do this we add \(2\) to both sides: \[\begin{align*} p-2 & =5\\ p-2+2 & =5+2\\ p & =7. \end{align*}\] The solution is \(p=7.\)
Example 3
Solve \(3g=18.\)
Solution: To make \(g\) the subject we need to divide both sides by \(3\): \[\begin{align*} 3g & =18\\ \frac{3g}{3} & =\frac{18}{3}\\ g & =6. \end{align*}\] The solution is \(g=6.\)
Example 4
Solve \(y/4=12.\)
Solution: To make \(y\) the subject we multiply both sides by \(4\): \[\begin{align*} \frac{y}{4} & =12\\ \frac{y}{4}\times4 & =12\times4\\ y & =48. \end{align*}\] The solution is \(y=48.\)
More Complex Equations
Some guidelines are:
With more complex equations it is necessary to perform several operations. As you become more experienced, you may perform several operations in one step.
If the variable appears in terms on both sides of the equation, you need to get these terms to one side of the equation and then solve for the variable.
If an equation involves brackets, the brackets should be expanded first.
If an equation involves fractions, you need to use a common denominator.
These ideas are illustrated in the following examples. Note that the strategy in the examples below is not part of the solution. It is the basic plan to solve the equation. You do NOT need to provide a strategy when solving problems. Nor do you need to describe each step. The strategy and description of each step is used below to show you the thinking that leads to the solution and the steps involved.
Example 5
Solve \(2w-3=-17.\)
Strategy: We want to make \(w\) the subject. We do this in two steps. First we get \(2w\) on its own then divide by two to get \(w\) as the subject. That is we add \(3\) to both sides and then divide both sides by \(2\).
Solution:
\[\begin{align*} 2w-3 & =-17\\ 2w-3+3 & =-17+3\\ 2w & =-14\\ \frac{2w}{2} & =-\frac{14}{2}\\ w & =-7. \end{align*}\] The solution is \(w=-7.\) With more complex equations, it is a good idea to check your result. However, this is not necessary unless you are asked to check. In this example, \[\begin{align*} \text{LHS} & =2w-3\\ & =2\times\left(-7\right)-3\\ & =-14-3\\ & =-17\\ & =\text{RHS } \end{align*}\] and so our solution is correct.
Example 6
Solve: \(\frac{3d}{4}+5=7.\)
Strategy: First get the term involving \(d\) on its own by subtracting five from both sides, then solve for \(d.\)
Solution: \[\begin{align*} \frac{3d}{4}+5 & =7\\ \frac{3d}{4}+5-5 & =7-5\quad\text{(subtract $5\text{ from both sides)}$ }\\ \frac{3d}{4} & =2\\ \frac{3d}{4}\times4 & =2\times4\quad\text{(multiply both sides by $4$ )}\\ 3d & =8\\ \frac{3d}{3} & =\frac{8}{3}\quad\text{(divide both sides by $3)$ }\\ d & =\frac{8}{3}. \end{align*}\] Solution is \(d=8/3.\)
We can check the solution (but this is not necessary) as follows: \[\begin{align*} \text{LHS} & =\frac{3d}{4}+5\\ & =\frac{3}{4}\times\frac{8}{3}+5\\ & =2+5\\ & =7\\ & =\text{RHS } \end{align*}\] so our solution is correct.
Example 7: Variable on Both Sides
Solve \(3c+1=c-5\).
Strategy: First get all the \(c\) terms on one side then solve for \(c\).
Solution: \[\begin{align*} 3c+1 & =c-5\\ 3c-c+1 & =c-c-5\quad\text{(subtract $c$ from both sides to get $c$ terms to one side)}\\ 2c+1 & =-5\\ 2c+1-1 & =-5-1\quad\text{(subtract $1$ from both sides)}\\ 2c & =-6\\ c & =-3\quad\text{(divide both sides by $2$ )}. \end{align*}\] The solution is \(c=-3.\)
Check (not required) \[\begin{align*} \text{LHS} & =3c+1\\ & =3\left(-3\right)+1\\ & =-8.\\ \text{RHS} & =c-5\\ & =-3-5\\ & =-8\\ & =\text{LHS } \end{align*}\] so our solution is correct.
Example 8: Brackets
Solve \(3(5-2j)=33.\)
Strategy: First remove brackets and solve using the techniques shown above.
Solution: \[\begin{align*} 3(5-2j) & =33\\ 15-6j & =33\quad\text{ (remove brackets) }\\ -6j & =33-15\quad\text{(subract $15$ from both sides)}\\ & =18\\ j & =\frac{18}{-6}\quad\text{(divide both sides by $-6$ )}\\ & =-3. \end{align*}\] The solution is \(j=-3.\)
Check (not required) \[\begin{align*} \text{LHS} & =3(5-2j)\\ & =15-6\left(-3\right)\\ & =15+18\\ & =33\\ & =\text{RHS} \end{align*}\] so our solution is correct.
Example 9: Brackets and Variable on Both Sides
Solve \(2(3k-2)=5\left(k+7\right).\)
Strategy: Remove brackets, get the variable on one side and then solve using the techniques shown above.
Solution: \[\begin{align*} 2(3k-2) & =5\left(k+7\right)\\ 6k-4 & =5k+35\\ 6k-5k-4 & =35\\ k-4 & =35\\ k & =35+4\\ & =39.\\ \\ \end{align*}\] The solution is \(k=39\).
Check (not required)
\[\begin{align*} \text{LHS} & =2\left(3k-2\right)\\ & =6k-4\\ & =6\times39-4\\ & =230.\\ \text{RHS} & =5\left(k+7\right)\\ & =5\left(39+7\right)\\ & =5\times46\\ & =230\\ & =\text{RHS } \end{align*}\] so our solution is correct.
Example 10: Fractions
Solve \(\frac{h+1}{3}=\frac{h}{4}\).
Strategy: Multiply both sides of the equation by a common denominator and solve using the techniques shown above. In this case a common denominator is \(12.\)
Solution: \[\begin{align*} \frac{h+1}{3} & =\frac{h}{4}\\ \left(\frac{h+1}{3}\right)\times12 & =\frac{h}{4}\times12\\ 4\left(h+1\right) & =3h\\ 4h-3h+4 & =0\\ h+4 & =0\\ h & =-4. \end{align*}\] The solution is \(h=-4.\)
Check (note required) \[\begin{align*} \text{LHS} & =\frac{h+1}{3}\\ & =\frac{-4+1}{3}\\ & =-1\\ \text{RHS} & =\frac{h}{4}\\ & =-1\\ & =\text{LHS} \end{align*}\] so our solution is correct.
Example 11
Solve \(\frac{2z+11}{7}=\frac{z-3}{12}\).
Strategy: A common denominator is \(84.\) So we multiply both sides by \(84\) and solve using the techniques shown above.
Solution: \[\begin{align*} \frac{2z+11}{7} & =\frac{z-3}{12}\\ \left(\frac{2z+11}{7}\right)\times84 & =\left(\frac{z-3}{12}\right)\times84\\ 12\left(2z+11\right) & =7\left(z-3\right)\\ 24z+132 & =7z-21\\ 24z-7z+132 & =-21\\ 17z+132 & =-21\\ 17z & =-21-132\\ & =-153\\ z & =\frac{-153}{17}\\ & =-9. \end{align*}\] The solution is \(z=-9.\)
Note that in this example, we have not put in all the details and explanation. This is what you should aim to do.
Example 12
Solve \(\frac{3u}{4}-\frac{1}{3}=7\).
Strategy: A common denominator is \(12.\) So we multiply both sides by \(12\) and solve using the techniques shown above.
Solution:
\[\begin{align*} \frac{3u}{4}-\frac{1}{3} & =7\\ \left(\frac{3u}{4}-\frac{1}{3}\right)\times12 & =7\times12\\ \frac{3u}{4}\times12-\frac{1}{3}\times12 & =84\\ 9u-4 & =84\\ 9u & =88\\ u & =\frac{88}{9}. \end{align*}\]
The last example is important as it shows that the solution may not be a whole number as in the previous examples.
Exercise 1
Solve the following equations.
\[\begin{array}{llrclllccc} a) & x+3=7 & & & b) & 5-j=-2 & & & c) & 3c=12\\ \\ d) & -r=-12 & & & e) & \frac{m}{2}=-7 & & & f) & -8u=12\\ \\ g) & 4g+4=16 & & & h) & 7-2w=1 & & & i) & \frac{e}{2}-5=-8\\ \\ j) & 21-3t=12 & & & k) & \frac{y}{5}-9=-5 & & & l) & 3-\frac{u}{2}=-7 \end{array}\]
\[\begin{array}{lcrcllcccccccccccccccccc} \textrm{1.} & a) & 4 & & b) & 7 & & c) & 4 & & d) & 12 & & e) & -14 & & f) & -\frac{3}{2} & & g) & 3 & & h) & 3\\ & i) & -6 & & j) & 3 & & k) & 20 & & l) & 20 \end{array}\]
Exercise 2
Solve these equations.
\[\begin{array}{llrclllccc} a) & 5i+2=i+10 & & & b) & 10p-11=2p-3 & & & c) & 5a-12=3a+6\\ \\ d) & 10d+10=0 & & & e) & f+6=6f-9 & & & f) & 8-g=5g+14\\ \\ g) & 5h-2=7h-12 & & & h) & 6j+13=4j+13 \end{array}\]
\[\begin{array}{lcrcllcccccccccccccccccc} \textrm{2.} & a) & 2 & & b) & 1 & & c) & 9 & & d) & -1 & & e) & 3 & & f) & -1 & & g) & 5 & & h) & 0\end{array}\]
Exercise 3
Solve
\[\begin{array}{llrclllccc} a) & 3(2k-4)=18 & & & b) & 5(2z+9)=15 & & & c) & 3(x+4)=6\\ \\ d) & 3(c+3)+2(c-5)=4 & & & e) & 3(2v-3)+2(v-4)=-25 & & & f) & 3(b+4)=2(4b+1) \end{array}\]
\[\begin{array}{lcrcllcccccccccccccccccc} \textrm{3.} & a) & 5 & & b) & -3 & & c) & -2 & & d) & 1 & & e) & -1 & & f) & 2\end{array}\]
Exercise 4
Solve
\[\begin{array}{llrclllccc} a) & \frac{9n}{5}-4=5 & & & b) & \frac{4m}{3}-11=9 & & & c) & 1-\frac{9q}{2}=-8\\ \\ d) & \frac{w-4}{2}=2 & & & e) & \frac{3-2e}{11}=1 & & & f) & \frac{3r+9}{5}=-3\\ \\ g) & \frac{3t}{8}+4=1 & & & h) & \frac{y}{3}=\frac{2}{9} & & & i) & \frac{5u-4}{4}=\frac{u-5}{5}\\ \\ j) & \frac{2i+1}{7}=\frac{3i-5}{4} & & & k) & \frac{p+1}{3}+1=4 & & & l) & 2-\frac{5a-4}{4}=4\\ \\ m) & \frac{d-3}{3}-4=\frac{d-2}{2} & & & n) & \frac{1-m}{5}-m=\frac{2m-1}{2} \end{array}\]
\[\begin{array}{lcrcllcccccccccccccccccc} \textrm{4.} & a) & 5 & & b) & 15 & & c) & 2 & & d) & 8 & & e) & -4 & & f) & -8 & & g) & -8 & & h) & \frac{2}{3}\\ & i) & 0 & & j) & 3 & & k) & 8 & & l) & -\frac{4}{5} & & m) & -24 & & n) & \frac{7}{22} \end{array}\]
Download this pdf document: ES1 Linear Equations (PDF 177 KB)
What's next... ES2 Simultaneous equations
