Electron configuration quiz
Take this quiz and test your knowledge of electron configuration.
Worked exercises
- Write the electron configuration of \(\ce{Si}\) using an orbital diagram (electrons in boxes notation).
Answer
Atomic number of \(\ce{Si}\) is \(14.\) Therefore, it has \(14\) electrons. These electrons should be placed in orbitals according to the Aufbau principle shown above. The first two electrons go to \(1s\) orbital as a pair. The next eight electrons are placed in the second shell (\(n=2)\) as pairs. The last four electrons enter into the third shell, where the first two occupy the \(s\) orbital as a pair and the last two fill two \(p\) orbitals as single electrons. - Write electron configuration of \(\ce{Ca}\) using noble gas configuration.
Answer
For \(\ce{Ca}\), \(\ce{Ar}\) is the last noble gas that comes before \(\ce{Ca}\). The electron configuration of \(\ce{Ca}\) is written as \(\left[\ce{Ar}\right]\) which denotes \(\ce{Ar}\)’s electron configuration followed by the configuration of remaning electrons.
\(Z=18\)\(\ce{Ar}\) \(1s^{2}\,2s^{2}2p^{6}\,3s^{2}3p^{6}\) (This is written as \(\ce{[Ar]}\) )
\(Z=20\)\(\ce{Ca}\) \(1s^{2}\,2s^{2}2p^{6}\,3s^{2}3p^{6}\,4s^{2}\) (After \(3p\) orbital, electrons fill into \(4s\) orbital not \(3d\) orbital.)
Noble gas configuration of \(\ce{Ca}\) is \(\left[\ce{Ar}\right]\) \(4s^{2}\) - How many electrons can an \(n=3\) shell accommodate?
- \(18\)
- \(10\)
- \(8\)
- \(2\)
- Which of the following subshells consist of one orbital?
- \(2p\)
- \(3d\)
- \(1s\)
- \(3p\)
- What is the maximum number of electrons that can occupy the \(2p\) subshell?
- \(2\)
- \(6\)
- \(10\)
- \(8\)
- What is the maximum number of electrons that can occupy one of the orbitals in the \(3d\) subshell?
- \(10\)
- \(6\)
- \(2\)
- \(8\)
- Which of the following statements is true?
- An electron in an \(n=1\) shell has lower energy than an electron in an \(n=2\) shell.
- All subshells contain same number of electrons
- The number of subshells within a shell is equal to the orbital number
- All subshells have an identical shape and size.
- What is the electron configuration of \(\ce{Cl}\) \(\left(Z=17\right)\)?
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{5}\)
- \(1s^{2}\:2s^{2}2p^{5}\:3s^{2}3p^{4}\)
- \(3s^{2}3p^{6}3d^{10}\)
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{2}3d^{3}\)
- What is the noble gas configuration of \(\ce{Na}\) \(\left(Z=11\right)\)?
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{1}\)
- \(\ce{[Ne]}\) \(3s^{1}\)
- \(\ce{[Ar]}\) \(3s^{1}\)
- \(\ce{[Ne]}\) \(s^{2}\:2s^{2}2p^{6}\:3s^{1}\)
- Which of the following is the orbital diagram of \(\ce{P}\) \(\left(Z=15\right)\)?
- What is the electron configuration of \(\ce{Fe}\) \(\left(Z=26\right)\)?
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{6}3d^{6}\:4s^{2}\)
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{6}3d^{8}\)
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{6}\:4s^{2}\)
- \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{6}3d^{6}\)
- How many unpaired electrons are present in the orbital diagram of \(\ce{N}\) \(\left(Z=7\right)\)
- \(5\)
- \(3\)
- \(7\)
- \(2\)
- Write the electron configuration of \(\ce{Na}\).
Answer
Atomic number of \(\ce{Na}\) is \(11.\) Therefore, it has \(11\) electrons. These electrons should be placed in orbitals according to the Aufbau principle shown below. The first two electrons go to \(1s\) orbital as a pair. The next two electrons are placed in the orbital \(2s\). The next six electrons are placed in \(2p\) orbitals as three pairs. The remaining electron is placed in \(3s\) orbital.
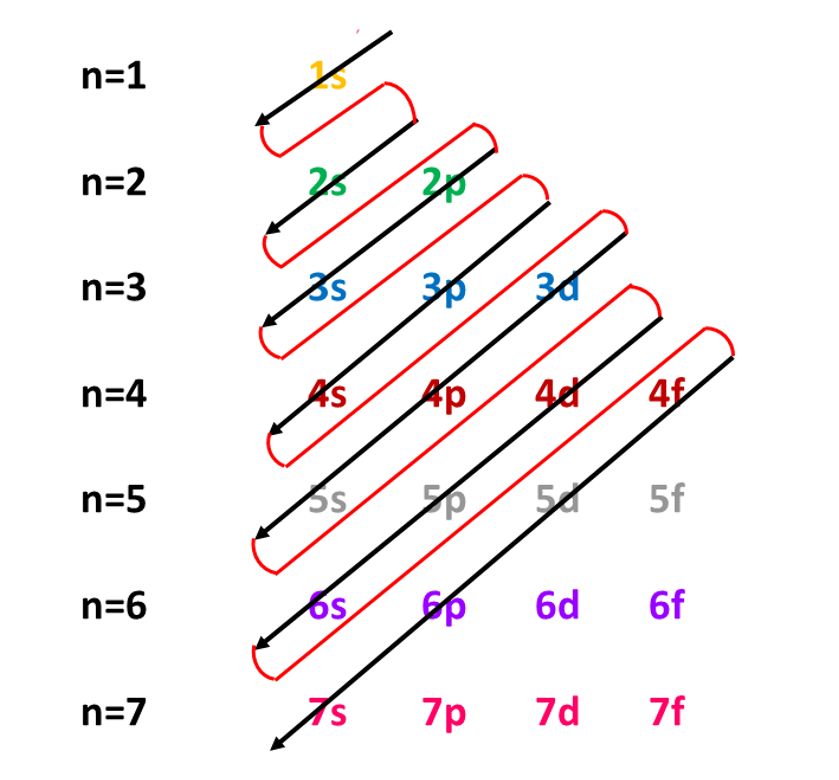
\(\ce{Na}\) has the configuration \(1s^{2}\,2s^{2}2p^{6}\,3s^{1}\)
- For an electron \(n=2\). What are the possible values for \(\ell\) and \(m_{\ell}\)?
Answer
For \(\ell\) permitted values are \(0,1,2,3\ldots\left(n-1\right)\). If \(n=2\), \(\ell\) can be \(0,1\).
\(\ell=0\) indicates a \(s\) orbital.
\(\ell=1\) indicates a \(p\) orbital.
\(\ell\) \(m_{\ell}\) \(0\) \(0\) \(1\) \(0,\,+1,\,-1\).
For \(\ell=0,\:m_{\ell}=0\) only: this defines one orbital.
In this case the \(2s\)-orbital.
For \(\ell=1,\:m_{\ell}=0,+1\) or \(-1\) only: this defines three separate orbitals. In this case, the three \(2p\) orbitals.
Exercises
1 \(18\)
3 \(1s\)
2 \(6\)
3 \(2\)
1 An electron in \(n=1\) shell has lower energy than an electron in \(n=2\) shell.
1 \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{5}\)
2 \(\ce{[Ne]}\) \(3s^{1}\)
a) The \(1s\),\(2s\),\(2p\),\(3s\) orbitals have paired electrons. The \(3p\) orbitals are occupied by one electron, each with the same spin.
1 \(1s^{2}\:2s^{2}2p^{6}\:3s^{2}3p^{6}3d^{6}\:4s^{2}\)
2 \(3\)
