D4 Rules for differentiation
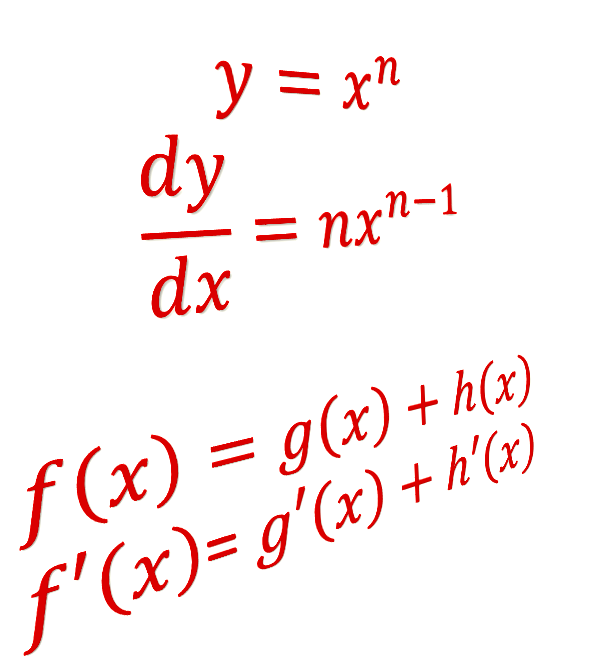
Learn about the rules for differentiation and the different notations that are used.
This section includes algebraic, exponential, logarithmic and trigonometric examples.
It is not always convenient to use differentiation from first principles to find a derivative function. The “rules” shown below have been established from first principles and can be used to find derivative functions directly.
Here’s a short video on differentiation. The general form is y equals x to the n. And if y equals x to the n, then the derivative, dydx, is nx to the n minus one. So if we have a function y equals x to the seven, then here n equals seven, hence dydx equals 7x to the 6th, because n minus one is seven minus one.
Let’s look at another example. Here we have two functions, y equals x³, plus x to the 6th. When we differentiate them we still differentiate them as though they were separate functions, in other words, x³ becomes three 8ths squared, and x to the 6th becomes 6x to the five, using the rule in the top right hand corner.
Let’s look at a trickier one. Here we have the function y equals one over x². Notice the x² is on the bottom of the fraction and this is quite difficult to do at this stage, so we now put x² up on the top. In other words, we remove the denominator and express it as x to the minus two. Now we have a negative index. And when we differentiate that n is now negative two. So the derivative dydx is negative two x to the negative three, because n minus one is minus two minus one. Notice we finally revert back to the fraction because x to the minus three is minus two over x³.
Let’s look at this function, y equals the square root of x. We express y equals the square root of x as an index so we write it as x to the half, and we always do this before we differentiate. Now proceeding with the differentiation, dydx will be a half x to the minus half, because here n is a half, so n minus one is a half minus one, which is minus a half. So our final answer is one over two to the square root of x.
Now let’s look at a more complicated fraction. The function here is now x to the four minus one, all over the square root of x. Here I’m breaking it up into two separate fractions, in other words, it’s x to the four over x to the half minus one over x to the half. Notice I’ve replaced the square root sign by an index. And now I write h to the four over h to the half as one term, which is x to the seven over two. One over x to the half is the same as x to the minus a half. In other words, I’m dividing through by x to the half.
The derivative is now calculated separably because we have two functions here to differentiate. So x to the seven over two becomes seven over 2x to the five over two, and x to the minus a half becomes a half x to the minus three over two. Notice we have two negative signs, one before the negative x and the index is negative a half, so the two negatives gives us a positive as our answer. So that we have the answer.
What about a derivative of a function which has a constant in front of it? K is the constant. If we have a constant in front of the function then the derivative is the constant multiplied by the rule that we’ve used before, nx to the n minus one. As a good example, the function here is y equals 7h to the six, so the derivative, dydx is seven, we leave the constant alone, and now we just differentiate h to the six, which becomes 6x to the five. The final answer is given by seven times 6x to the five. Seven sixes are 42, so the answer is now 42x to the five.
Finally, the derivative of a function which is simply a constant. So here if y equals a constant, then the derivative is always zero. Probably the easiest one of the lot to remember. In other words, if you have any number which is a constant, such as 99, y equals 99, then the derivative is equal to zero.
Now try some questions for yourself. Here are 10 questions that I want you to differentiate. The answers are on the next slide. Thanks for watching this video.
Alternative Notations
We will also introduce alternative notations for derivatives. When \(y\) is a function of \(x\), i.e. \(y=f(x)\), the derivative function may be written as \(y'\) or \(\frac{dy}{dx}\) or \(f'(x)\).
It is important to understand that \(d/dx\) is a symbol that means “take the derivative of something with respect to \(x\)”. For example \[\begin{align*} \frac{d}{dx}\left(x^{2}\right) \end{align*}\] means take the derivative of \(x^{2}\) with respect to \(x.\)
Operational Rules
Here are some rules for these are essential and underlie much of what you will use in your course. In this section we present the rules and give some examples.
- If \(g(x)=kf(x)\), where \(k\) is a constant then \[\begin{align*} g'(x) & =kf'(x) \end{align*}\]
or \[\begin{align*} \frac{dg}{dx} & =k\frac{df}{dx}. & \left(1\right) \end{align*}\]
- If \(f(x)=k,\) where \(k\) is a constant then \[\begin{align*} f'(x) & =0 & \left(2\right) \end{align*}\]
- If \(f(x)=g(x)+h(x)\) then \[\begin{align*} f'(x) & =g'(x)+h'(x) \end{align*}\]
or \[\begin{align*} \frac{df}{dx} & =\frac{dg}{dx}+\frac{dh}{dx} & \left(3\right) \end{align*}\]
- Derivative of a power of \(x\). If \(y=x^{n}\), where \(n\) is a real number, then \[\begin{align*} \frac{dy}{dx} & =nx^{n-1}. & \left(4\right) \end{align*}\]
Examples
If \(y=x^{7},\) find \(dy/dx.\)
sing operational rule \(\left(4\right)\) we have \[\begin{align*} \frac{dy}{dx} & =7x^{7-1}\\ & =7x^{6}. \end{align*}\]If \(y=x^{2000},\) find \(dy/dx.\)
Solution:
Using operational rule \(\left(4\right)\) we have \[\begin{align*} \frac{dy}{dx} & =2020x^{2020-1}\\ & =2020x^{2019}. \end{align*}\]If \(y=\sqrt{x}\) , find \(dy/dx\).
Solution:
First write \(y\) in index form: \[\begin{align*} y & =\sqrt{x}\\ & =x^{1/2}. \end{align*}\] Now apply operational rule \(\left(4\right)\) \[\begin{align*} \frac{dy}{dx} & =\frac{1}{2}x^{\frac{1}{2}-1}\\ & =\frac{1}{2}x^{-\frac{1}{2}}\\ & =\frac{1}{2\sqrt{x}}. \end{align*}\]If \(y=1/x^{2}\), find \(dy/dx.\)
Solution:
First write \(y\) in index form: \[\begin{align*} y & =1/x^{2}\\ & =x^{-2}. \end{align*}\] Now apply operational rule \(\left(4\right)\) \[\begin{align*} \frac{dy}{dx} & =-2x^{-2-1}\\ & =-2x^{-3}\\ & =-\frac{2}{x^{3}}. \end{align*}\]If \(y=x^{3}+7x^{6}\), find \(dy/dx.\)
Solution:
Using operational rule \(\left(3\right)\), \[\begin{align*} \frac{dy}{dx} & =\frac{d}{dx}\left(x^{3}\right)+\frac{d}{dx}\left(7x^{6}\right). \end{align*}\] Now applying operational rule \(\left(4\right)\) to the first terms on the right we have \[\begin{align*} \frac{dy}{dx} & =3x^{2}+\frac{d}{dx}\left(7x^{6}\right). \end{align*}\] The second term to the right is dealt with using operational rule \(\left(1\right)\) and so \[\begin{align*} \frac{dy}{dx} & =3x^{2}+7\frac{d}{dx}\left(x^{6}\right)\\ & =3x^{2}+42x^{5}. \end{align*}\]If \(y=\frac{4}{x}\) +10, find \(dy/dx.\)
Solution:
Convert to index form \[\begin{align*} y & =4x^{-1}+10. \end{align*}\] Then using operational rules \(\left(4\right)\)and \(\left(3\right)\) \[\begin{align*} \frac{dy}{dx} & =-4x^{-2}+\frac{d}{dx}\left(10\right). \end{align*}\] Applying operational rule \(\left(2\right)\)to the last term on the right gives:
\[\begin{align*} \frac{dy}{dx} & =-\frac{4}{x^{2}}+0\\ & =-\frac{4}{x^{2}}. \end{align*}\]If \(f\left(x\right)=\) \(\frac{x^{4}-1}{\sqrt{x}}\) find \(f'(x)\).
Solution:
First convert to index form \[\begin{align*} f\left(x\right) & =\frac{x^{4}-1}{x^{1/2}}, \end{align*}\] then divide through by \(x^{1/2}\) to get \[\begin{align*} f\left(x\right) & =x^{4-\frac{1}{2}}-x^{-1/2}\\ & =x^{7/2}-x^{-1/2}. \end{align*}\] Applying operational rules \(\left(3\right)\) and \(\left(4\right)\) we have \[\begin{align*} f'\left(x\right) & =\frac{7}{2}x^{\frac{7}{2}-1}-\left(-\frac{1}{2}\right)x^{-\frac{1}{2}-1}\\ & =\frac{7}{2}x^{\frac{5}{2}}+\frac{1}{2}x^{-\frac{3}{2}}. \end{align*}\]
Derivatives of Some Other Functions
The table below gives derivatives for particular functions. Using the table and the rules above we ca expand the functions that we can differentiate.
| Function | Derivative |
|---|---|
| \(f(x)=e^{x}\) | \(f'(x)=e^{x}\) |
| \(f(x)=\log_{e}x\) | \(f'(x)=\frac{1}{x}\) |
| \(f(x)=\textrm{sin}\left(x\right)\) | \(f'\) \((x)=\textrm{cos}\left(x\right)\) |
| \(f(x)=\textrm{cos}\left(x\right)\) | \(f'\)(\(x)=-\sin\left(x\right)\) |
| \(f(x)=\textrm{tan}\left(x\right)\) | \(f'(x)=\sec^{2}x\) |
Examples
If \(y=\textrm{sin}\left(x\right)+3x^{2}\) then \(dy/dx\) =\(\textrm{cos}\left(x\right)+6x\).
If \(y=e^{x}-5\) then \(dy/dx=e^{x}.\)
If \(y=10\left(\cos\left(x\right)-\frac{1}{2x}\right)\) then \[\begin{align*} \frac{dy}{dx} & =10\left(-\sin\left(x\right)-\frac{1}{2}\left(-1\right)x^{-2}\right)\\ & =-10\sin\left(x\right)+\frac{10}{2}x^{-2}\\ & =-10\sin\left(x\right)+\frac{5}{x^{2}}. \end{align*}\]
Exercises
- Differentiate the following
\[\begin{array}{ccccc} \textrm{a})\,y=x^{7} & \textrm{ b})\,y=x^{\frac{1}{5}} & \mathscr{\textrm{c}})\,y=x^{-19} & \textrm{d})\,y=\frac{1}{x^{4}} & \textrm{e})\,53\\ \textrm{f})\,y=\sqrt[4]{x} & \textrm{g})\,5x^{6} & \textrm{h})\,y=9x^{-5} & \textrm{i})\,\frac{\sqrt{5}}{x} & \textrm{j})\,3x^{2}+2x \end{array}\]
\[\begin{array}{ccccc} 1.\ \textrm{a})\,7x^{6} & \textrm{b})\,\frac{1}{5x^{\frac{4}{5}}} & \textrm{c})-19x^{-20} & \textrm{d})-\frac{4}{x^{5}} & \textrm{e})\,0\\ \textrm{ f})\,\frac{1}{4}x^{-\frac{3}{4}} & \textrm{g})\,30x^{5} & \textrm{h})-45x^{-6} & \textrm{i})\,\frac{-\sqrt{5}}{x^{2}} & \textrm{j})\,6x+2 \end{array}\]
- Find the derivatives of
a)\(\,\sin\left(x\right)-\cos\left(x\right)\quad\text{b)$\,10-\log_{e}\left(x\right)\quad\text{c) $\tan\left(x\right)-\sqrt{x}\quad\text{d) $3\cos x-\frac{1}{x^{2}}\quad\text{e) $\frac{e^{x}}{6}-x^{7}.$ }$ }$ }$ }\)
2 a) \(\cos x+\sin x\quad\)b) \(-\frac{1}{x}\quad\)c) \(\sec^{2}\left(x\right)-\frac{1}{2\sqrt{x}}\quad\)d) \(-3\sin\left(x\right)+\frac{2}{x^{3}}\quad\)e) \(\frac{e^{x}}{6}-7x^{6}.\)
Download this page, D4 Rules for Differentiation (PDF 189KB)
What's next... D5 The chain rule
