D12 Implicit differentiation
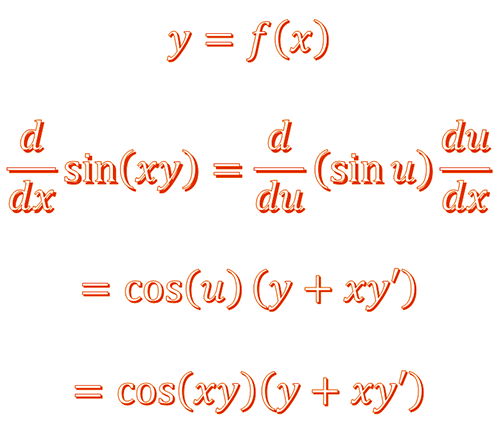
Implicit differentiation enables you to find the derivative of y with respect to x without having to solve the original equation for y.
If we are able to write an equation relating \(x\) and \(y\) explicitly, that is in the form \(y=f(x)\), then we can find the derivative function \(y=f'\left(x\right)\) or \(y=\) \(\frac{dy}{dx}\) using the rules we have learned so far.
For example, if \[\begin{align*} y & =3x^{2}-2x+5 \end{align*}\] then \[\begin{align*} \frac{dy}{dx} & =6x-2. \end{align*}\]
But how do we differentiate expressions such as \(y^{5}+3xy+x^{2}-5=0\) or find \(\frac{d}{dx}\left(sin(xy)\right)\)?
In such expressions \(y\) is said to be an implicit function of \(x\) as we cannot rearrange the expression to the form \(y=f(x)\). But we can use implicit differentiation techniques to find \(\frac{dy}{dx}\) without having to solve the given equation for \(y\).
Within this process the chain rule must be used whenever the function \(y\) is being differentiated because it is assumed that \(y\) is an unknown function of \(x\).
The Chain Rule
Consider \(\frac{d}{dx}\left(y^{2}\right)\)
If \(y=\sin(x),\) \(\frac{d}{dx}\left(y^{2}\right)\) becomes \(\frac{d}{dx}\left([\sin(x)]^{2}\right)\). Applying the chain rule \(\frac{dy}{dx}=2\sin(x)\cdot\cos(x)=2y\cdot\frac{dy}{dx}\)
If \(y=(4x+3)\), \(\frac{d}{dx}\left(y^{2}\right)\) becomes \(\frac{d}{dx}(4x+3)^{2}\). Applying the chain rule \(\frac{dy}{dx}=2(4x+3)\cdot4=2y\cdot\frac{dy}{dx}\)
If \(y=e^{x},\) \(\frac{d}{dx}\left(y^{2}\right)\) becomes \(\frac{d}{dx}\left(e^{x}\right)^{2}\).
Applying the chain rule \(\frac{dy}{dx}=2\left[(e^{x})\right]\cdot e^{x}=2y.\frac{dy}{dx}\)
And when \(y\) is an unspecified function of \(x,\) \(\frac{d}{dx}\left(y^{2}\right)=2y\cdot\frac{dy}{dx}\)
More generally, using the chain rule, if \(u=f(y)\) then \[\begin{align*} \frac{du}{dx} & =\frac{du}{dy}\cdot\frac{dy}{dx}. & \left(1\right) \end{align*}\]
Example 1
Find \(\frac{d}{dx}\left(y^{2}x\right)\).
Solution:
Using the product rule first
\[\begin{align*} \frac{d}{dx}\left(y^{2}x\right) & =y^{2}\frac{d}{dx}(x)+x\frac{d}{dx}(y^{2})\\ & =y^{2}\cdot1+x\frac{d}{dy}\left(y^{2}\right)\frac{dy}{dx}\ \text{using $\left(1\right)\text{ above}$ }\\ & =y^{2}+x\cdot2y\frac{dy}{dx}\\ & =y^{2}+2xy\frac{dy}{dx}. \end{align*}\]
Example 2
Find \(\frac{dy}{dx}\) if \(y^{3}=2xy-7\). 1 \(\frac{dy}{dx}\) may be abbreviated by \(y'\). Sometimes this is helpful in reducing the amount you have to write. In this example we use \(\left(1\right)\) on the left hand side and the product rule on the term \(2xy.\)
Solution:
\[\begin{align*} y^{3} & =2xy-7\\ 3y^{2}y' & =2x\cdot1y'+2\cdot1\cdot y-0\\ 3y^{2}y' & =2xy'+2y\\ 3y^{2}y'-2xy' & =2y\\ (3y^{2}-2x)y' & =2y\\ y' & =\frac{2y}{3y^{2}-2x}. \end{align*}\]
Example 3
Find the value of the derivative at the point \(\left(\pi,0\right)\) if \(\sin\left(xy\right)=2x.\)
Solution:
We have \[\begin{align*} \sin\left(xy\right) & =2x. \end{align*}\] Using the chain rule on \(\sin\left(xy\right)\) and the product rule on \(xy\) we obtain \[\begin{align*} \cos\left(xy\right)\cdot\left(xy'+y\right) & =2\\ \textrm{At}\ (\pi,0),\,\cos(\pi\cdot0)\cdot\left(\pi y'+0\right) & =2\\ \left(1\right)\cdot\left(\pi y'\right) & =2\\ \pi y' & =2\\ y' & =\frac{2}{\pi}. \end{align*}\]
Example 4
Find the equation of the tangent line to the circle \(x^{2}+y^{2}=9\) at the point \((2,\sqrt{5})\).
Solution:
Differentiating implicitly, we have \[\begin{align*} 2x+2yy' & =0\\ y' & =\frac{-2x}{2y}\\ & =-\frac{x}{y}. \end{align*}\] At the point \((2,\sqrt{5})\), \(y'\) and so the gradient \(m\) of the tangent is \[\begin{align*} m & =-\frac{2}{\sqrt{5}}. \end{align*}\] Hence the equation of the tangent is2 Remember that the equation of a straight line with gradient \(m\) through the point \(\left(x_{1},y_{1}\right)\) is \[\begin{align*} y-y_{1} & =m\left(x-x_{1}\right). \end{align*}\]
\[\begin{align*} y-\sqrt{5} & =-\frac{2}{\sqrt{5}}\left(x-2\right)\\ y & =-\frac{2}{\sqrt{5}}x+\frac{4}{\sqrt{5}}+\sqrt{5}\\ & =-\frac{2}{\sqrt{5}}x-\frac{1}{\sqrt{5}}\left(4+5\right)\\ & =-\frac{2}{\sqrt{5}}x+\frac{9}{\sqrt{5}}. \end{align*}\]
Exercises
\(1.\ \)Find \(\frac{d}{dx}\left(\frac{x}{y}\right)\). Hint: use quotient rule.
\(\frac{y-xy'}{y^{2}}\).
\(2.\ \)Find\(\frac{d}{dx}\left(\frac{x+y}{x-y}\right).\)
\(\frac{2xy'}{\left(x-y\right)^{2}}\).
\(3.\ \)Find the value of \(\frac{dy}{dx}\) at the point (1, 2) if \(x^{2}+y=7-2xy\).
\(-2.\)
\(4.\ \)Find \(\frac{dy}{dx}\) if e\(^{x}\) \(\sin(y)\) = \(x\) .
\(\frac{e^{x}-1}{cosy}\).
\(5.\ \)Find the equation of the tangent line to the circle \(x^{2}+y^{2}=4\) at the point \((1,\sqrt{3})\).
\(y=-\frac{1}{\sqrt{3}}x+\frac{4}{\sqrt{3}}.\)
Download this page, D12 Implicit Differentiation (PDF 172KB)
What's next... D13 Partial differentiation
