Units for structural principles



Units of measurement

The units of measurement for structural calculations are based on the SI units (International System of Units).

Basic units have lower case letters as their symbol such as m for metre, g for gram.

Prefixes are also used for larger or smaller values of a basic unit:

A millimetre (mm) is one thousandth of a metre and a kilogram (kg) is 1000 grams.

Many of the units used in structural calculations are combinations of two or more other basic units. These are often complex and confusing to write, so they are given a name. Usually the name is based on some prominent person within that field of study, eg newton (N), pascal (Pa) etc.

These units have an upper case letter to denote them, for example:

Top

Units of force

By definition, force = mass x acceleration or F = ma

The unit of acceleration is metres per second per second (m/s/s) or metre per second squared (m/s2). If the acceleration is gravity, the acceleration is 9.8 metres per second squared (9.8 m/s2). This figure is sometimes rounded off to 10 m/s2 which builds in a conservative factor of 2% on all load calculations.

So the units of force (in F = ma) are:

F = kg x m/s2 or kg.m/s2

This unit of force has been given the name newton (N).

A force of 1 N is the force when an acceleration of 1 m/s2 acts on a mass of 1 kg.

1 N = 1 kg x 1 m/s2

The force produced by 1 kg when acted on by gravity is: 1 kg x 10 m/s2 = 10 N

From this it follows thatwill produce a force of 1 N.

This is a very small unit compared to the weight of a structure. Therefore a larger more useable unit is required. In structures the unit used is the kilonewton (kN) where:

1 kN = 1,000 N

Therefore to convert mass to force units (kN) suitable for structural calculations:


Top

Units of pressure

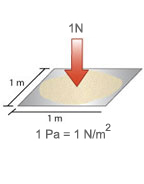
Other loads that occur on buildings may be due to loads spread evenly over an area creating pressure. One such pressure is wind load which is the pressure wind exerts on a structure. The basic unit measurement for pressure is the pascal (Pa).

Pressure is force per unit area.

1 Pa = 1 N/m2, ie one newton per square metre

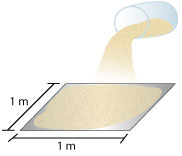
Image of a glass pouring sand on to a sheet with the area of 1 m x 1 m.

To get some idea of the size of one pascal, imagine 100 g of sand (about ½ cup) spread evenly over an area of 1 m2. This is the pressure exerted by one pascal. This unit is far too small for most structural calculations, therefore the larger units of kilopascals (kPa) and megapascals (MPa) are used.

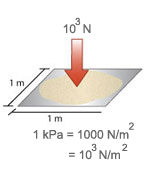
A kilopascal is 1,000 N/m2, ie 1 kPa = 1,000 N/m2

and 1,000 N = 1 kN

so 1 kPa = 1 kN/m2

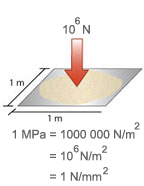
The megapascal is 1,000,000 N/m2 and there are 1,000,000 mm2 in 1 m2.

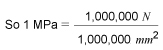
1 MPa = 1 N/mm2, ie one newton per square millimetre

Three diagrams of sheets with the area of 1 m x 1 m. The first sheet has sand on it and there is a glass pouring sand onto the sheet. At the middle of the sheet is a red arrow pointing down. On top of the arrow is the label 1 N. Below the sheet is the equation 1 Pa = 1 N/m2. Three diagrams of sheets with the area of 1 m x 1 m. The second sheet has sand on top of it and at the middle of the sheet there is a red arrow pointing downwards. On top of the arrow is the label 103N. Below the sheet is the equation 1 kPa = 1000 N/m2, which equals 103 N/m2. Three diagrams of sheets with the area of 1 m x 1 m. The third sheet has sand on top of it and at the middle of the sheet there is a red arrow pointing downwards. On top of the arrow is the label 106N. Below the sheet is the equation 1 MPa = 1,000,000 N/m2 which equals 106 N/m2, which equals 1 N/mm2.

Top